用二叉链表做为存储结构，先序遍历算法可描述为:

void InOrder(BinTree T)

{ //算法里①~⑥是为了说明执行过程加入的标号

① if(T) { // 如果二叉树非空

② printf("%c"，T->data); // 访问结点 ③ InOrder(T->lchild); ④ InOrder(T->rchild); ⑤ }

⑥ } // InOrder

void createBiTree(BiTree *bt){

char ch;

ch = getchar();

if(ch == '.')

*bt = NULL;

else{

*bt = (BiTree)malloc(sizeof(BiTNode));//向内存申请节点空间

(*bt)->data = ch;

createBiTree(&((*bt)->LChild));//生成左子树

createBiTree(&((*bt)->RChild));//生成右子树

}

}/*createBiTree*/

/*==================打印二叉树=============*/

void printTree(BiTree bt,int nLayer){

int i;

if(bt == NULL)

return ;

printTree(bt ->RChild,nLayer+1);

for(i=0;i<nLayer;i++)

printf(" ");

printf("%c\n",bt->data);

printTree(bt->LChild,nLayer+1);

}

图一:

(a)1 2 4 . . 6 . . 3 . 5 . 7 . 8 . .

(b)1 2 4 . . 5 . . 3 6 . . 7 . . 运行结果:

图二:

(a)7 3 1 . . 2 . . 9 . 10 . 8 . 4 . .

(b)7 3 1 . . 5 4 . . . 11 10 . . 15 . .

运行结果:

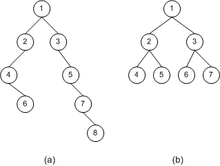
用C语言最简单的哈夫曼算法实现

#include <stdio.h>

#include <conio.h>

struct BinaryTree

{

long data;

int lchild,rchild;

};

//定义一个二叉树结构

void sort(struct BinaryTree cc[],int l,int r);

void xx(long kk,struct BinaryTree cc[]);

void zx(long kk,struct BinaryTree cc[]);

void hx(long kk,struct BinaryTree cc[]);

//对函数的声明

main(void)

{

struct BinaryTree Woods[101];

long i,j,n,xs,k;

scanf("%d",&n);

for ( i=1; i<=n; ++i)

{

scanf("%d",&Woods.data);

Woods.lchild=0;

Woods.rchild=0;

} //依次读入权值

k=n;

xs=1;

--n;

while (k>1)

{

sort(Woods,xs,n+1);

Woods[n+2].data=Woods[xs].data+Woods[xs+1].data; //将根结点权值为左子树也右子树权值之和

Woods[n+2].lchild=xs; //对左子树和右子树的设置

Woods[n+2].rchild=xs+1;

++n;

xs=xs+2;

--k;

} //哈夫曼算法

printf("%s","preorder:");

xx(n+1,Woods);

printf("\n%s","inorder:");

zx(n+1,Woods);

printf("\n%s","postorder");

hx(n+1,Woods);

printf("\n"); //输出先序,中序,后序序列

getch();

}

//快速排序

void sort(struct BinaryTree cc[],int l,int r)

{

long x,y;

int i,j,rc,lc;

i=l;

j=r;

x=cc[(l+r)/2].data;

if (r<l)

return;

do

{

while(cc.data<x)

++i;

while(x<cc[j].data)

--j;

if (i<j)

{

y=cc.data;

rc=cc.rchild;

lc=cc.lchild;

cc.data=cc[j].data;

cc.lchild=cc[j].lchild;

cc.rchild=cc[j].rchild;

cc[j].data=y;

cc[j].lchild=lc;

cc[j].rchild=rc;

++i;

--j;

}

}

while(i>j);

if (i<r)

sort(cc,i,r);

if (j>l)

sort(cc,l,j);

}

//先序序列

void xx(long kk,struct BinaryTree cc[])

{

if (cc[kk].data!=0)

{

printf("%d%c",cc[kk].data,' ');

if (cc[kk].lchild!=0)

xx(cc[kk].lchild,cc);

if (cc[kk].rchild!=0)

xx(cc[kk].rchild,cc);

}

}

//中序序列

void zx(long kk,struct BinaryTree cc[])

{

if (cc[kk].data!=0)

{

if (cc[kk].lchild!=0)

zx(cc[kk].lchild,cc);

printf("%d%c",cc[kk].data,' ');

if (cc[kk].rchild!=0)

zx(cc[kk].rchild,cc);

}

}

//后序序列

void hx(long kk,struct BinaryTree cc[])

{

if (cc[kk].data!=0)

{

if (cc[kk].lchild!=0)

hx(cc[kk].lchild,cc);

if (cc[kk].rchild!=0)

hx(cc[kk].rchild,cc);

printf("%d%c",cc[kk].data,' ');

}

}

将一个普通的中序表达式转换为逆波兰表达式的一般算法是:

首先需要分配2个栈，一个作为临时存储运算符的栈S1(含一个结束符号)，一个作为输入逆波兰式的栈S2(空栈)，S1栈可先放入优先级最低的运算符#，注意，中缀式应以此最低优先级的运算符结束。可指定其他字符，不一定非#不可。从中缀式的左端开始取字符，逐序进行如下步骤:

(1)若取出的字符是操作数，则分析出完整的运算数，该操作数直接送入S2栈

(2)若取出的字符是运算符，则将该运算符与S1栈栈顶元素比较，如果该运算符优先级大于S1栈栈顶运算符优先级，则将该运算符进S1栈，否则，将S1栈的栈顶运算符弹出，送入S2栈中，直至S1栈栈顶运算符低于(不包括等于)该运算符优先级，最后将该运算符送入S1栈。

(3)若取出的字符是"("，则直接送入S1栈顶。

(4)若取出的字符是")"，则将距离S1栈栈顶最近的"("之间的运算符，逐个出栈，依次送入S2栈，此时抛弃"("。

(5)重复上面的1~4步，直至处理完所有的输入字符

(6)若取出的字符是"#"，则将S1栈内所有运算符(不包括"#")，逐个出栈，依次送入S2栈。

完成以上步骤，S2栈便为逆波兰式输出结果。不过S2应做一下逆序处理。便可以按照逆波兰式的计算方法计算了!