我和平面几何的50年感情
——另类回忆录,朝花夕拾其乐融融!/6531刘卓

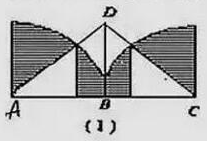
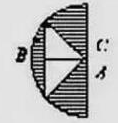
说来好笑,我和平面几何的50年感情,是从一道数学题卡壳开始的。那是1962年夏天的中考,数学试卷的最后一题是几何作图:已知一个直角三角形的一个直角边,另一直角边和斜边之和,求作这个直角三角形。当时我无论如何想不出来怎么做,绞尽脑汁,就是不知道怎么下手,只好坐在那里发呆,手心还有点冒汗。走出考场一问,原来十分简单。先用已知的直角边,另一直角边和斜边之和作一个过渡的直角三角形,再在这个直角三角形的斜边上作中垂线,交大直角边于一点,连接这一点和底边的顶点,即得所求的直角三角形。(见图1)

这事对我刺激很大,因为在这之前,好像还没有发生过有什么题完全不会做的(井底之蛙,不知道外面世界的深浅!)。追究起来,初中母校也没有什么可以责备的地方,因为那时候全国三年自然灾害时期,饭都吃不饱,处处讲究劳逸结合,各种课程当中,能够精简的就省略不讲了,连课本都是用回收纸印刷的,呈一种淡淡的灰黑色。我记得几何书就特别简单,一看就懂,没有复杂难做的题目。
进入高中以后就想,这样不行呀,万一今后高考出一道平面几何题,怎么办?于是在1962年冬天,咬咬牙,花9毛钱到交通路旧书店,淘到一本严济慈编的《几何证题法》。9毛钱当时可是一笔大钱,要知道香喷喷的烧饼才3分钱一个,大烧饼5分钱一个。并且手头只有唯一的这一本参考书,于是从头啃到尾,一字不漏,所有习题统统做光。学习几何最有效的方法就是做题,通过书里面各种各样的杂题,使你从不同的角度,对每个定理有了透彻的理解。所谓“熟读唐诗300首,不会吟诗也会吟”,慢慢的,我对做几何题,也有两刷子了。这里面还有一个难忘的回忆:做题的草稿纸极其稀缺。每学期开学的时候,只能从家里拿到1角4分钱,到长江日报的红旗大楼边门,在那里买1斤印刷厂的边角余料,当草稿纸,这1斤草稿纸数理化都要用,并且要一直用到本学期结束。所有的空白地方都要写满,舍不得浪费!
当时我们1班的男生,大部分坐在后排,偶尔偷偷的互相递纸条,求解数学难题。有一天,一位学友突然递给我一道题:求作一个三角形,使与已知三角形相似,并且3个顶点分别在3个同心圆的圆周上。大概用了二十来分钟,我就把做法写出来了。思路是:先画图,假设已经作出,这个题的关键点是同心圆的圆心,把圆心分别连接到三角形的3个顶点,关系就看出来了。因为这3条连线的长度分别是3个半径R1,R2,R3, 所以圆心到3个三角形顶点的距离之比分别是R1/R2, R2/R3, R3/R1,这样作法就出来了:对已知三角形ABC的两条边,作比值为R1/R2, R2/R3的两个阿氏圆,它们相交于P点,连接PA, PB, PC, 得到角1和角2,再以同心圆的圆心为顶点,画出角1和角2,它们的3条边与3个圆周交于D, E, F, 三角形DEF即为所求。(见图2)

做出来以后,我的心情好极了。这证明我也可以做难题,不比别人差。慢慢的,别人也会对你刮目相看了!后来我打听到,上面的题目,是上海市数学会编的《高中数学复习资料》里面的一道题,没有具体答案。(该书只有计算题才有答案。)自此以后,对几何题愈发勤奋起来,每天做,一步一步越来越投入,好像上了瘾。虽然高二,高三的课程内容和平面几何渐行渐远,越来越搭不上关系,但每天晚上临睡以前还是要看一,二页几何,放松一下子。几何图形的精美和纯粹的逻辑思维,令人陶醉。不过对于考试来讲,后来的高考没有出现过平面几何题,往后的一辈子,也没有用过什么复杂的几何图形。它实际上是个花瓶子,好看而不实用(工程技术中用途不大)。
1965年离开一中后,在军校军训、学习了一年,就开始搞文化大革命,到处都是大字报。但我对“造反”,还是“保皇”,始终没有什么兴趣。既不想关心“国家大事”,也不想“把无产阶级文化大革命进行到底”。好在学校图书馆那几年管理松懈,几乎无人问津。这样我就隔三差五的跑到书库里面,“窃”几本书,看完以后偷偷送回去,接着再“窃”几本。3年中间看了许多好书。至今还记得的,有郭沫若的《中国史稿》,商务印书馆编辑的《四角号码新词典》,日本长泽龟之助的《几何学词典》。其中《几何学词典》洋洋大观,有1寸半厚,1千多页,题目上万,全部分门别类,详列解法,并配精美图形。令你不得不对这位老先生肃然起敬。记得该书的译者叫薛德炯,吴载耀,他们在前言中说:(30年代的中国)“文艺小说,车载斗量,科学作品,寥若晨星”。这话我到现在都记得,因为它说出了中国社会的特点,切中时弊。当然到现在,文艺小说已经不看了,大家都玩手机,这在地铁里面是一道亮丽的风景线。
到了七、八十年代,比较好的几何书有香港秦元勲的几何学概论,该书用东亚人特有的简洁手法(不谈严谨),介绍平面几何中一些最重要定理的证明路径,特别适合业余爱好者的胃口。我国数学老前辈李儼先生的《近世几何学初编》,以及德国希尔伯特《直观几何》,从不同的视角,全方位地介绍平面几何在数学中的地位(和其他分支的关系),读来令人振奋。
这其中值得一提的是帕斯卡定理,叙述如下:圆内接六边形3双对边的交点共线。当我仔细看完证明以后,不禁拍案叫好,这个定理太漂亮了,你看,只要圆上有6个任意点,就可以形成3双对边,就有3个交点,这3点就一定在一条直线上!这是一个精确的函数关系:前提是圆(也包括椭圆),结论是3点共线。证明中间,4次使用同一个预备定理,并不复杂,关键要会看图。这个定理是帕斯卡300多年以前发现的,当时他才16岁,后来他终身未娶,只活了30多岁,晚年放弃科学,专心研究神学。这使我怀疑,真正的数学天才,都是上帝派他们下凡的,向人间泄漏了一些天机以后,又匆匆把他们召回天上。像伽罗华,阿贝尔都有类似的经历,都是英年早逝。与帕斯卡定理互为对称的,有布利安桑定理,也很漂亮:圆外切六边形3双顶点的连线共点。你看,只要把两个定理中间的“内接—外切”,“点—线”互换位置,句型不变,就变成了和它对偶的定理。这符合数学美的基本要求:简单,对称,精准。我个人认为,这两个定理是平面几何中间,最精致、最完美的定理。它把点、直线、圆的关系镶嵌得天衣无缝。(见图3)

2001年4月5日,武汉晚报第3版,刊登一则数学题的征解结果。它是当时的国家领导人访问澳门的时候,对中学生出的一道平面几何题:“任意五角星,分别作5个角的外接圆,得5个外接圆的5个交点,求証这5点共圆。”我在翻报纸的时候,看到这个题,觉得有些趣味。再仔细看了一下,想起它在法国数学家阿达玛的《几何学教程》中间出现过,赶紧拿书一翻,果然有,于是照抄以后,向武汉晚报投稿。结果在4月5日的征解结果里面,竟然有我的大名,是15个正确解答者之一,不过是排在最后一名。奖品是2支精装圆珠笔,尽管微乎其微,我还是很高兴。要知道,它是我这辈子学习平面几何唯一的物质奖励呀!(见图4和武汉晚报的照片)


等到2006年正式退休前后,因为无事可做,闲得慌,又看了两本比较好的几何书,一本是日本林鹤一先生所著《初等几何学作图不能问题》,(1935年版),另一本是美国约翰逊著《近代欧氏几何学》。特别前一本书,很值得一看。虽然文言文甚为拗口,并且许多数学名词的翻译与现代相差太远,但是内容十分精彩,可读性很高。除了我们熟悉的古典三大不可能问题(化圆为方,立方倍积,三等分角)以外,对所有仅用圆规直尺不可能作出的几何图形,分门别类进行了归纳和分析,上升到理论高度,使人不留悬念。最为精彩的是等分圆周这一章。我们在中学里已经知道怎么样3等分圆周,5等分圆周。再往上,7等分?11等分?13等分?……因为人的大脑有限,已经搞糊涂了,所以从古希腊到现在,没有人再前进一步。直到1777年高斯诞生,他在18岁时一举解决了这个问题,指出下一个可以等分的圆周,是17等分,并且以后在他的墓碑上面,画的就是一个正17边形。高斯证明,只有当边数为费马数时,(即2的2的n次方加1,像3,5,17,257,
65537…)正多边形才可能用圆规直尺作出来。
具体讲,有人根据他的理论,采用代数方法在单位圆上,对17边形每个顶点的值进行复数计算,最后用直尺圆规画出正17边形。数学史记载,后人作257边形,用了16页纸,再有人作65537边形,用了一皮箱纸!可见18、19世纪,人们对这个理论的痴迷及对高斯的崇拜。
2009年,我到德国旅游的时候,曾经专门驱车2个小时,到哥廷根大学,瞻仰高斯故居和他长期工作过的哥廷根天文台,他在那儿主持了一次历史上著名的大地测量,企图验证非欧几何学的基本结论:三角形的内角和不等于180度,但是失败了。同行的德国朋友说我是高斯的粉丝,我很高兴:“对呀,我就是高斯的粉丝!”
从遥远的东方,来了一个黄皮肤黑头发的人,瞻仰高斯。多么富有诗意!这说明中国的国力已经变得强大,普通老百姓也可以到欧洲来,瞻仰伟大的科学巨人!下面的照片是我在高斯的青铜像前留影,坐者是高斯,站立者是韦伯(物理学家)。

邓丽君有一首家喻户晓的歌曲:“……路边的野花不要采!”可我一辈子就喜欢不断的采集各种各样的野花野草,想方设法去沾花惹草。当然,它们是数学大花园里面的绚丽花卉、几何学的奇花异草,不是什么别的东西。大家不要想歪了!
把优美的几何题比做美丽的花朵,不是我的发明创造。北京师范大学的梁绍鸿先生,在1958年编写了一本中国的经典:《初等数学复习及研究(平面几何)》,今年再版印刷的时候,后人这样赞美它:“愿几何世界中的琼花瑶草迎风绽放,来点缀美丽芬芳的数学百花园。”
除此之外,学习几何对我还另有妙用:治病,催眠。人的一生,难免遇到各种各样的困境和挫折,导致情绪烦躁,郁闷。每到此时,我就习惯性的拿一本几何书,看他几页,正所谓“两耳不闻窗外事,闭门只读圣贤书”,用不了多长时间,血压自然下降,情绪慢慢平静下来,又能心平气和地看待周围的现实世界了。它的效果和散步或者打球差不多,甚至更好。有时候白天兴奋过度,晚上也很难入睡,这时候又拿几何题来看它几眼,不管会不会做,不会做更好,很快脑筋就进入迷糊状态,昏昏入睡。要是还睡不着,就在心中默念:“你这辈子一事无成,但是你努力了,你曾经奋斗过,你可以心安理得……”等等,诸如此类的话,能从心理上产生奇妙的催眠效果,马上身心放松,进入南柯梦乡,极少尝到失眠之苦。所以,各位可以看出,我毕生养成的这个优雅的嗜好:和平面几何有50年亲密接触,不仅有回报的,并且是很丰厚的回报。
(转自新浪博客)

 免费!!!高中数学竞赛平面几何定理证明大全
免费!!!高中数学竞赛平面几何定理证明大全

 几何变换思想
几何变换思想