两平面间的距离h称为厚度，和两平面等距的平面称为板的中面，中面上的区域为，,h比起，的最小直径小一个数量级时，就是薄板.弹性力学平面应力问题的对象，在外形上也是薄板，但通常指的薄板问题，是指它的外载荷垂直于中面，它的变形主要是弯曲变形.描述它的变形通常用中面上点的法向上的位移表示，这个位移称为挠度.令中面所在的平面为xy平面，则挠度w(x,y)满足方程

式中q(x,y)为分布荷载，D=Eh3/12(1-vZ)称为板的抗弯刚度，E为杨氏模量，v为泊松比，Oz为双调和算子.板的挠度方程在适当的边条件下可以求解，通常是在二的边界上给定挠度w、绕边界转角awan弯矩从己和剪力Q，四个量中的两个，Mn和Q，可以表示为w的微分表达式.如果在板的边界上作用有板面内的外力，板内的应力可以由弹性力学平面应力问题求解得到，设为。二，ay , rs,,，则这时板的挠度方程为

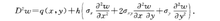
板的弯曲问题，在工程上有许多应用，求解它比较困难，经常采用近似方法和数值方法.弹性薄板问题，除了求解平衡问题外，还有振动、稳定性等其他问题.