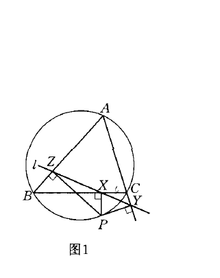
1.从三角形的外接圆上任一点向三边所在直线作垂线,则三个垂足在同一直线上.这条直线称为西姆森线或称垂足线.如图1,P是△ABC外接圆上任一点,X,Y,Z是从点P分别向BC , CA , AB所引垂线的垂足,X,Y,Z同在△ABC的西姆森线上.
2.完全四边形的米奎尔点在四边上的正射影在同一条直线上.这条直线称为完全四边形的西姆森线.如图2中,M是完全四边形ADBCE的米奎尔点,X,Y,Z,K分别是M在边AB,BC,DE,AE上的正射影,X,Y,Z,K同在完全四边形的西姆森线m上.通常认为关于三角形的西姆森线是西姆森(Simson ,R.)发现的,后经马开(Mackay)考证表明,该直线是1797年由华莱士(Wallace, W.)发现的.但习惯上仍称西姆森线.