选择特殊符号

Ф δ ° × # Ⅱ Ⅲ ½ ¼

选择搜索类型

市场价信息价参考价询价供应商云知资讯文库百科

造价通

请输入搜索

首页 > 百科 > 建设工程百科

缓和曲线

缓和曲线指的是平面线型中，在直线与圆曲线、圆曲线与圆曲线之间设置的曲率连续变化的曲线。缓和曲线是道路平面线形要素之一，它是设置在直线与圆曲线之间或半径相差较大的两个转向相同的圆曲线之间的一种曲率连续变化的曲线。《公路工程技术标准》（JTG B01-2014）规定，除四级路可不设缓和曲线外，其余各级公路都应设置缓和曲线。在现代高速公路上，有时缓和曲线所占的比例超过了直线和圆曲线，成为平面线形的主要组成部分。在城市道路上，缓和曲线也被广泛地使用。

缓和曲线基本信息

中文名缓和曲线
外文名transition curve
类型道路平面线形要素
出处《公路工程技术标准》
性质曲率连续变化的曲线

缓和曲线缓和曲线线型

缓和曲线的线型多种多样，如回旋线、三次抛物线、七次四项式型、半波正弦型、一波正弦型、双纽线、多心复曲线…… 我国常用的线型有两种：三次抛物线、回旋线。其中三次抛物线是回旋线的近似结果。 缓和曲线三次抛物线 铁路上常用的缓和曲线是三次抛物线型。其方程式为： 上式中 是三次抛物线参数，它越大缓和曲线越缓。它近似的等于圆曲线半径乘以缓和曲线长度，即 三次抛物线型缓和曲线的优点是铺设和养护维修比较容易，缓和曲线长度比较短；其缺点是始、终点存在折角，影响行车的平稳性。 缓和曲线回旋线 公路、匝道常用的缓和曲线是回旋线，也叫放射螺旋线。回旋线不仅线形美观，而且与驾驶员匀速转动方向盘由圆曲线驶入直线或者由直线驶入圆曲线的轨迹线相符合。 回旋线的本质特征是： 即曲率 随弧长 线性变化； 表示曲率随弧长的增大而增大或减小； 是回旋线参数。它是圆曲线半径 R 与缓和曲线全长 的几何平均值，单位为米。对于一条缓和曲线而言，它是一个常数。A 越大，说明曲率变化越慢，曲线拐弯越缓；A越小，说明曲率变换越快，曲线拐弯越急。

查看详情

缓和曲线造价信息

市场价
信息价
询价

曲线拉板

规格型号：
品种:曲线拉板;说明:铁附件;类型:曲拉板;外形尺寸(mm):40×4×250;表面处理:热镀;
价格行情：
材料单位：
副
材料品牌：
浩川
材料税率：
13%
供应商：
银川浩川电力设备有限公司
报价时间：
2022-12-08

查看价格

曲线锯

规格型号：
品种:曲线锯;规格型号:GST85PBE;
价格行情：
材料单位：
台
材料品牌：
博世
材料税率：
13%
供应商：
宁夏聚多丰商贸有限公司
报价时间：
2022-12-08

查看价格

曲线锯

规格型号：
品种:曲线锯;类型:木工工具;规格:MIQ-FF-85;
价格行情：
材料单位：
台
材料品牌：
东成
材料税率：
13%
供应商：
内蒙古鑫利达五金交电有限公司
报价时间：
2022-12-08

查看价格

曲线锯

规格型号：
品种:曲线锯;类型:木工工具;规格:GST 25 M;
价格行情：
材料单位：
台
材料品牌：
博世
材料税率：
13%
供应商：
内蒙古鑫利达五金交电有限公司
报价时间：
2022-12-08

查看价格

曲线锯

规格型号：
品种:曲线锯;规格型号:MIQ-FF-85;包装规格:8台/箱;
价格行情：
材料单位：
台
材料品牌：
东成
材料税率：
13%
供应商：
青铜峡市杰达电动工具商行
报价时间：
2022-12-08

查看价格

查看详情

钢筋弯曲机

规格型号：
HBG-12
价格行情：
材料单位：
台·月
材料税率：
地区时间：
深圳市2020年6月信息价
所属行业：
建筑工程
备注说明：

查看价格

钢筋弯曲机

规格型号：
HBG-12
价格行情：
材料单位：
台·月
材料税率：
地区时间：
深圳市2020年5月信息价
所属行业：
建筑工程
备注说明：

查看价格

钢筋弯曲机

规格型号：
HBG-12
价格行情：
材料单位：
台·月
材料税率：
地区时间：
深圳市2019年9月信息价
所属行业：
建筑工程
备注说明：

查看价格

钢筋弯曲机

规格型号：
HBG-12
价格行情：
材料单位：
台·月
材料税率：
地区时间：
深圳市2019年4月信息价
所属行业：
建筑工程
备注说明：

查看价格

钢筋弯曲机

规格型号：
HBG-12
价格行情：
材料单位：
台·月
材料税率：
地区时间：
深圳市2019年3月信息价
所属行业：
建筑工程
备注说明：

查看价格

查看详情

曲线攀爬

规格型号：
详见图纸
需求量：
1个
报价数：
3
材料品牌：
-
材料档次：
中高档
费用说明：
不含税费 | 含运费
询价时间：
2022-08-19

查看价格

曲线卧房灯

规格型号：
JXD-WH132-35 32W曲线卧房灯
需求量：
440个
报价数：
1
材料品牌：
嘉美时代
材料档次：
中档
费用说明：
含税费 | 不含运费
询价时间：
2015-12-21

查看价格

曲线卧房灯

规格型号：
JXD-WH140-35 40W曲线卧房灯
需求量：
9778个
报价数：
1
材料品牌：
嘉美时代
材料档次：
中档
费用说明：
不含税费 | 含运费
询价时间：
2015-04-13

查看价格

曲线卧房灯

规格型号：
JXD-WH122-35 22W曲线卧房灯
需求量：
8876个
报价数：
1
材料品牌：
嘉美时代
材料档次：
中档
费用说明：
不含税费 | 不含运费
询价时间：
2015-07-06

查看价格

手提曲线锯

规格型号：
博世(BOSCH)GST800手提曲线锯功率:710W;空载
需求量：
1台
报价数：
1
材料品牌：
博世（BOSCH）GST800手提曲线锯
材料档次：
中档
费用说明：
含税费 | 含运费
询价时间：
2019-05-30

查看价格

查看详情

缓和曲线曲线要素

实地放样缓和曲线之前，需要计算若干曲线要素： 不同类型的缓和曲线，数值不同 不同类型的缓和曲线，数值不同 不同类型的缓和曲线，数值不同 上面的公式中 ——路线偏转角，单位：弧度。这是设计数据； R——圆曲线半径，单位：m。这是设计数据； ——缓和曲线偏转角，单位：弧度； p——内移距，单位：m； q——切线增长，单位：m；（有些文献用 m 表示该变量） T——切线长，单位：m； E——外距，单位：m； D——切曲差，即切线长减去曲线长，单位：m； 注意： 的计算公式请见下文，每种类型的缓和曲线都有自己的计算公式。 [式中 α 为路线设计参数，R值对于设计道路可查相关规范]

查看详情

缓和曲线缓和曲线的作用

缓和曲线的作用： 1、缓和曲率——使曲率连续变化； 2、缓和超高——使横向坡度连续变化； 3、缓和加宽——使车道加宽连续变化。 缓和曲线产生的效果： 1、曲率连续变化，便于车辆驾驶； 2、离心加速度连续变化，没有突变，乘客感觉舒适； 3、超高横坡度及加宽逐渐变化，行车更加稳定； 4、与圆曲线配合，增加线形美观。

查看详情

缓和曲线常见问题

缓和曲线怎么算？

5800手机应该不行，电脑上可以CAD 使用SPLINE命令。
怎样在CAD中绘出缓和曲线

工具栏有样条曲线工具
求一份公路缓和曲线计算原理或公式推理？

我也在找，有的时候分享一下

查看详情

缓和曲线缓和曲线长度

由于直线与圆曲线间存在曲率半径的突变，圆曲线半径越大，这种突变程度就越小。当圆曲线半径超过2000m时，这种突变对轨道交通行车影响很小。而当正线上曲线半径不大于2000m时，则要在圆曲线与直线间加设缓和曲线，实现曲率半径的逐渐过渡，减少列车在突变点处的轮轨冲击。因此，《地铁设计规范》（GB50157—2003）规定：“线路平面圆曲线与直线之间应根据曲线半径、超高设置及设计速度等因素设置缓和曲线，其长度可按表的规定采用。” 地铁缓和曲线长度 R/L/.V 100 95 90 85 80 75 70 65 60 55 50 45 40 35 30 3000 30 25 20 2500 35 30 25 20 2000 40 35 30 25 20 20 1500 55 50 45 35 30 25 20 1200 70 60 50 40 35 30 25 20 20 1000 85 70 60 50 45 35 30 25 25 800 85 80 75 65 55 45 40 35 30 25 20 700 85 80 75 70 60 50 45 35 30 25 20 20 650 85 80 75 70 60 55 45 40 35 30 25 20 20 600 85 75 70 70 60 50 45 35 30 20 20 20 550 75 70 70 65 55 45 40 35 20 20 20 500 70 70 65 60 50 45 35 20 20 20 20 450 70 65 60 55 50 40 25 20 20 20 400 65 60 60 55 45 25 20 20 20 350 60 60 60 35 30 25 20 20 20 300 60 60 60 35 30 25 20 20 250 60 60 40 35 30 20 20 200 60 40 40 35 25 20 150 40 40 35 25

查看详情

缓和曲线详论回旋线

回旋线最本质的特点就是 为了确定上式的正负号，需要对曲率的正负号取值做个约定 缓和曲线曲率符号 数学上曲率的定义为 ，即曲率是前进方位角T随弧长l的变化率。 在 的情况下，若 则k取正值，若 则k取负值。 下图分四种情况，对曲率的正负号取法进行了说明： 曲率半径是曲率的倒数，其符号与曲率一致。 缓和曲线曲率变化率 公式 中，参数A无法反映出曲率随弧长增大，到底是增大还是减小？为此引入常量a，它满足下式 a就是曲率变化率，它可能是正数，也可能是负数。 a与A的关系满足公式 为了说明a的符号，以及它与A的关系，请见下图 在测量坐标系下K0 000处的曲率为-1/100(左转为负)，K0 150处的曲率为1/50（右转为正）。可知： 曲率变化率 参数 在数学坐标系下K0 000处的曲率为1/100(左转为正)，K0 150处的曲率为-1/50（右转为负）。可知： 曲率变化率 参数 缓和曲线微分方程通解 求解微分方程 可得 曲率k随桩号L变化的函数为 。当 时 前进方向T随桩号L变化的函数为 。当 时 坐标随桩号L变化的函数为（用到了复数）： 当 时 特别的，当 时 缓和曲线微分方程特解 当 时，令 ，则 这个特解与通解相比，简化了不少。它的含义其实就是在曲率为零的地方建立坐标系。如下图所示，在直缓点建立了坐标系： x轴是回旋线的切线，其正方向是桩号增加方向；y轴是回旋线的法线，在x轴的左边就是数学坐标系，在x轴的右边就是测量坐标系。 从原点开始沿回旋线行走距离 ，到达点P，其坐标为(x，y)。 点 P 处的切线与轴夹角为 ，称其为切线角，也是点 P 处的前进方位角。 原点与点 P 的连线叫弦，其长度为c，也就是弦长。 原点到点 P 的方位角为 ，也就是偏角，也叫弦切角。 点 P 处，切线与弦线的夹角为 从原点开始沿回旋线行走距离 ，到达缓圆点HY，即回旋线的长度为 圆曲线的半径为R 在缓圆点处达到最大值 接下来，计算各个参数： 曲率变化率 参数 曲率 曲率半径 切线角 最大切线角 坐标 弦长的计算公式如下： 弦切角的计算公式如下： 注意： 亦即弦切角近似的等于切线角的三分之一。 缓和曲线要素 回旋线的曲线要素计算公式如下： 缓和曲线道路正算 回旋曲线段，根据桩号 L，距中 Z，计算前进方向 T 及坐标 x，y的公式如下： 上式需要一个起算点，即需要知道桩号 处的 。也可以从曲率为零的点开始起算，根据 可知：当 时曲率为零。 是回旋线上任意一点的桩号和曲率。 距中 Z 的正方向是前进方向 T 加上90°，因此： 在数学坐标系下，距中 Z 左正右负，即在回旋线沿桩号增加方向右侧取负值； 在测量坐标系下，距中 Z 左负右正，即在回旋线沿桩号增加方向左侧取负值。

查看详情

缓和曲线详论三次抛物线

缓和曲线参数C 参数 C 按下式计算： 更高次项的系数，请见下表 1 2/5 1123/3600 23519/78000 93134377/286416000 671176607/1790100000 60632952362431/134042688000000 10959451729410359/19436189760000000 28568328624908898433/39649827110400000000 596762934176757576209/635718894670080000000 2098157146254959366777509639/1688977959359468544000000000 14062585980252142453129239257/8444889796797342720000000000 3127534025901397259312263980851/1386126739060529356800000000000 上式中，R 是圆曲线的曲率半径。它是有正负号的，具体取法请参考前文； 是缓和曲线长度，注意它也是有正负号的：顺着前进方向为正，逆着前进方向为负。现举例说明，如下图所示 以ZH点为原点的坐标系是测量坐标系，将根据 HY 点计算C。从 ZH 至 HY（桩号增加的方向）右转，因此HY处的曲率半径 R 取正值。HY 点的桩号比 ZH 点的桩号大，所以 Ls 也取正值。最终 C 为正值。 以HZ点为原点的坐标系是数学坐标系，将根据 YH 点计算C。从 YH 至 HZ（桩号增加的方向）右转，因此YH处的曲率半径 R 取负值。YH 点的桩号比 HZ 点的桩号小，所以 Ls 也取负值。最终 C 为正值。 注意：使用上述规则时，要求x 轴必须是切线，而且其正方向是桩号增加的方向。 更为一般的计算公式为： 上式中： 是三次抛物线上任意一点的曲率半径， 是该点的桩号减去曲率为零点的桩号。 缓和曲线坐标 x 坐标 x 按下式计算 更高次项的系数，请见下表 1 -1/40 23/5760 -2773/2995200 2066579/8146944000 -224209943/2932899840000 28747533091/1173159936000000 -261175434475093/31844253302784000000 86647036511116753/30570483170672640000000 -2316511336548771758119/2307460069722370867200000000 35677500215657115786212861/98390097372961893777408000000000 缓和曲线坐标 y 坐标y 按下式计算 更高次项的系数，请见下表 1/6 -1/80 133/57600 -16933/29952000 23345441/146644992000 -95319797/1955266560000 13001597946211/823558275072000000 -1694382133343581/318442533027840000000 9603494098034819239/5196982139014348800000000 缓和曲线曲率 曲率按下式计算： 更高次项的系数，请见下表 1 -2/5 121/720 -3337/46800 1932763/63648000 -579833/44752500 1585042411/286416000000 -9194722916339/3887237952000000 943636378388861/932937108480000000 -1904209296741873383/4401130809254400000000 69481023021498242079629/375328435413215232000000000 -11534698506084794283343/145601548220643840000000000 16035089603343026034099263/472913828620651192320000000000 缓和曲线曲率半径 曲率半径等于曲率的倒数 缓和曲线切线角 切线角按下式计算： 更高次项的系数，请见下表 1/2 -1/15 121/7200 -3337/655200 1932763/1145664000 -579833/984555000 1585042411/7446816000000 -9194722916339/116617138560000000 943636378388861/31719861688320000000 -1904209296741873383/167242970751667200000000 69481023021498242079629/15763794287355039744000000000 -11534698506084794283343/6697671218149616640000000000 16035089603343026034099263/23645691431032559616000000000000 缓和曲线最大切线角 最大切线角按下式计算 更高次项的系数，请见下表 1/2 2/15 167/1800 46351/546000 25385099/286416000 5252428289/52509600000 3982854295663/33510672000000 4270501632677849/29154284640000000 7356042227375864101/39649827110400000000 11595993887859194946607/48314635994926080000000 1866776187030795889021687763/5911422857758139904000000000 233123111824877589842938537/553368847083586560000000000 114262828881514570894054876308869 /200988377163776756736000000000000 缓和曲线弦长 弦长按下式计算 更高次项的系数，请见下表 1 -1/90 7/3240 -1021/1895400 -103137467/148478054400 1824489697/267260497920000 1962656897729/320712597504000000 172597317854624597/17410845493297152000000 12570996329063196101/12535808755173949440000000 -84559611892561668247007/73412289685903166668800000000 986086453888432129684636273/2402965612958834641128652800000000 缓和曲线弦切角 弦切角按下式计算： 更高次项的系数，请见下表 1/6 -4/405 329/194400 -279619937/50948352000 49981690783/400890746880000 -10875344672639/352783857254400000 112198229967587/11545653510144000000 -142446483534146625839/18803713132760924160000000 52613217024783269917249/38359574790832285286400000000 3424580749757991824764543627/15532865900902135616451379200000000 -1413931320131094500306391029838659/32941774994930072328304475504640000000000 缓和曲线最大弦切角 最大弦切角按下式计算 更高次项的系数，请见下表 1/6 23/405 2033/48600 1740762847/50948352000 10960255204399/400890746880000 6772270615585369/352783857254400000 1193239078444885151/150093495631872000000 -161805233310981385370591/18803713132760924160000000 -1286980164945796856981760287/38359574790832285286400000000 -72056068243648037753159483098122901/1009636283558638815069339648000000000 -4238353071056815709683515980381542179491/32941774994930072328304475504640000000000 -562636180723418426132797552941934630463/2614426586899212089547974246400000000000 -232168897210836372569220251035298614709587903/672012209896573475497411300294656000000000000 缓和曲线要素 更高次项的系数，请见下表 0 1/24 -19/1920 -9139/691200 -3240559/159744000 -282589603597/8798699520000 -7026310366847/140779192320000 -19235406274658191/253402546176000000 -1157743059288068176933/10190161056890880000000 -31472972322721395868013113/187091357004516556800000000 -593565174736535737082257554883/2399758472511265701888000000000 -2404682875032206089252747022332201/6641331572674927829975040000000000 -1872334767018224961225647555546981/3542043505426628175986688000000000 更高次项的系数，请见下表 1/2 -11/80 -5321/57600 -52487/7488000 18677834707/146644992000 3188362247677/9776332800000 169430712200037851/274519425024000000 332286113603292440329/318442533027840000000 8671309730283052493037077/5196982139014348800000000 912479043985584874133797609/352905657722244956160000000 696256490101343458284600171876781/177102175271331408799334400000000 13074672153106612908209529164613637/2213777190891642609991680000000000 463819829160454637226871854554498260583/52687897143221094117801984000000000000 2100433B

查看详情

缓和曲线文献

不对称缓和曲线隧道详细测设及放样

格式：pdf

大小：279KB

页数： 2页

不对称缓和曲线隧道详细测设及放样——我国现行隧道设计规范规定，三级和三级以上隧道在隧道路线转弯时，要设置曲线，对于一般地形通常设置为对称曲线，但在特殊地形或受地物限制时，可设置不对称缓和曲线．关于不对称曲线的计算，相关书籍都有各自的算法，根据...

在线阅读立即下载

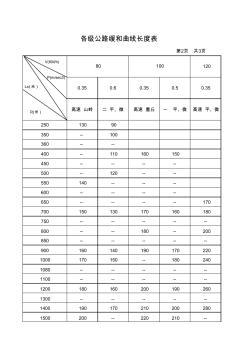各级公路缓和曲线长度表

格式：pdf

大小：279KB

页数： 2页

120 0.35 0.6 0.35 0.5 0.35 高速山岭二平、微高速重丘一平、微高速平、微 250 130 90 350 -- 100 360 -- -- 400 -- 110 160 150 450 -- -- -- -- 500 -- 120 -- -- 550 140 -- -- -- 600 -- -- -- -- 650 -- -- -- -- 170 700 150 130 170 160 180 750 -- -- -- -- -- 800 -- -- 180 -- 200 850 -- -- -- -- -- 900 160 140 190 170 220 1000 170 150 -- 180 240 1080 -- -- -- -- -- 1100 -- -- -- -- -- 1200 180 160 200 190 260 1300

在线阅读立即下载

道路平面缓和曲线

当汽车从直线地段驶入曲线时，为了缓和行车方向的突变和离心力的突然发生和消失，并能使汽车不减速而平稳地通过，在平曲线两端采用适应汽车转向和离心力渐变的缓和曲线，用来连接直线和平曲线。 缓和曲线主要有三种线形，即回旋线(辐射螺旋线)、双纽线和三次抛物线。较理想的缓和曲线是汽车从直线段驶入一定半径的平曲线时，在不降低车速又能徐缓均匀转向的情况下，即汽车转弯的曲率半径从无穷大，有规律地逐渐减小至平曲线半径，其中回旋线较能符合上述要求。 按照等速行驶、等角速度转动方向盘的条件，求得的曲线称为回旋曲线。在回旋线方程中，如果近似地以曲线弦长代替弧长，就成为双纽线。如果近似地以曲线沿切线的长度代替弧长，就成为三次抛物线。

查看详情

缓和曲线测设简介

中文名称 缓和曲线测设 英文名称 spiral curve location;transition curve location 定　　义 把设计的连接直线与圆曲线、圆曲线与圆曲线之间设置的曲率半径连续变化的曲线放于实地的测量工作。 应用学科 测绘学（一级学科），工程测量（二级学科）

查看详情

道路缓和曲线一般设置在哪儿？

缓和曲线曲率连续变化，便于车辆遵循；离心加速度逐渐变化，旅客感觉舒适；超高横坡度及加宽逐渐变化，行车更加平稳；与圆曲线配合，增加线形美观。 缓和曲线设置在直线和圆曲线之间或半径相差较大的两个转向相同的圆曲线之间。 《规范》规定：除四级公路外的其它各级公路都应设置缓和曲线，另外，当圆曲线半径大于“不设超高的最小半径”时可省略缓和曲线。

查看详情

热门搜索

缓和曲线

缓和曲线基本信息

缓和曲线三次抛物线

缓和曲线回旋线

缓和曲线造价信息

曲线拉板

曲线锯

曲线锯

曲线锯

曲线锯

钢筋弯曲机

钢筋弯曲机

钢筋弯曲机

钢筋弯曲机

钢筋弯曲机

曲线攀爬

曲线卧房灯

曲线卧房灯

曲线卧房灯

手提曲线锯

缓和曲线常见问题

缓和曲线曲率符号

缓和曲线曲率变化率

缓和曲线微分方程通解

缓和曲线微分方程特解

缓和曲线要素

缓和曲线道路正算

缓和曲线参数C

缓和曲线坐标 x

缓和曲线坐标 y

缓和曲线曲率

缓和曲线曲率半径

缓和曲线切线角

缓和曲线最大切线角

缓和曲线弦长

缓和曲线弦切角

缓和曲线最大弦切角

缓和曲线要素

缓和曲线文献

相关推荐