1 Fundamental Equations of Laminated Beams,Plates and Shells.
1.1 Three-Dimensional Elasticity Theory in Curvilinear Coordinates
1.2 Fundamental Equations of Thin Laminated Shells
1.2.1 Kinematic Relations
1.2.2 Stress-Strain Relations and Stress Resultants
1.2.3 Energy Functions
1.2.4 Governing Equations and Boundary Conditions
1.3 Fundamental Equations of Thick Laminated Shells
1.3.1 Kinematic Relations
1.3.2 Stress-Strain Relations and Stress Resultants
1.3.3 Energy Functions
1.3.4 Governing Equations and Boundary Conditions
1.4 Lamé Parameters for Plates and Shells.
2 Modified Fourier Series and Rayleigh-Ritz Method
2.1 Modified Fourier Series
2.1.1 Traditional Fourier Series Solutions.
2.1.2 One-Dimensional Modified Fourier Series Solutions
2.1.3 Two-Dimensional Modified Fourier Series Solutions
2.2 Strong Form Solution Procedure
2.3 Rayleigh-Ritz Method (Weak Form Solution Procedure)
3 Straight and Curved Beams
3.1 Fundamental Equations of Thin Laminated Beams
3.1.1 Kinematic Relations
3.1.2 Stress-Strain Relations and Stress Resultants
3.1.3 Energy Functions
3.1.4 Governing Equations and Boundary Conditions
3.2 Fundamental Equations of Thick Laminated Beams.
3.2.1 Kinematic Relations
3.2.2 Stress-Strain Relations and Stress Resultants
3.2.3 Energy Functions
3.2.4 Governing Equations and Boundary Conditions
3.3 Solution Procedures
3.3.1 Strong Form Solution Procedure
3.3.2 Weak Form Solution Procedure (Rayleigh-Ritz Procedure)
3.4 Laminated Beams with General Boundary Conditions
3.4.1 Convergence Studies and Result Verification
3.4.2 Effects of Shear Deformation and Rotary Inertia
3.4.3 Effects of the Deepness Term (1 z/R).
3.4.4 Isotropic and Laminated Beams with General Boundary Conditions.
4 Plates
4.1 Fundamental Equations of Thin Laminated Rectangular Plates.
4.1.1 Kinematic Relations
4.1.2 Stress-Strain Relations and Stress Resultants
4.1.3 Energy Functions
4.1.4 Governing Equations and Boundary Conditions
4.2 Fundamental Equations of Thick Laminated Rectangular Plates.
4.2.1 Kinematic Relations
4.2.2 Stress-Strain Relations and Stress Resultants
4.2.3 Energy Functions
4.2.4 Governing Equations and Boundary Conditions
4.3 Vibration of Laminated Rectangular Plates
4.3.1 Convergence Studies and Result Verification
4.3.2 Laminated Rectangular Plates with Arbitrary Classical Boundary Conditions
4.3.3 Laminated Rectangular Plates with Elastic Boundary Conditions.
4.3.4 Laminated Rectangular Plates with Internal Line Supports.
4.4 Fundamental Equations of Laminated Sectorial, Annular and Circular Plates
4.4.1 Fundamental Equations of Thin Laminated Sectorial, Annular and Circular Plates
4.4.2 Fundamental Equations of Thick Laminated Sectorial, Annular and Circular Plates
4.5 Vibration of Laminated Sectorial, Annular and Circular Plates
4.5.1 Vibration of Laminated Annular and Circular Plates
4.5.2 Vibration of Laminated Sectorial Plates
5 Cylindrical Shells
5.1 Fundamental Equations of Thin Laminated Cylindrical Shells
5.1.1 Kinematic Relations
5.1.2 Stress-Strain Relations and Stress Resultants
5.1.3 Energy Functions
5.1.4 Governing Equations and Boundary Conditions
5.2 Fundamental Equations of Thick Laminated Cylindrical Shells
5.2.1 Kinematic Relations
5.2.2 Stress-Strain Relations and Stress Resultants
5.2.3 Energy Functions
5.2.4 Governing Equations and Boundary Conditions
5.3 Vibration of Laminated Closed Cylindrical Shells
5.3.1 Convergence Studies and Result Verification
5.3.2 Effects of Shear Deformation and Rotary Inertia
5.3.3 Laminated Closed Cylindrical Shells with General End Conditions
5.3.4 Laminated Closed Cylindrical Shells with Intermediate Ring Supports
5.4 Vibration of Laminated Open Cylindrical Shells
5.4.1 Convergence Studies and Result Verification
5.4.2 Laminated Open Cylindrical Shells with General End Conditions
6 Conical Shells.
6.1 Fundamental Equations of Thin Laminated Conical Shells
6.1.1 Kinematic Relations
6.1.2 Stress-Strain Relations and Stress Resultants
6.1.3 Energy Functions
6.1.4 Governing Equations and Boundary Conditions
6.2 Fundamental Equations of Thick Laminated Conical Shells
6.2.1 Kinematic Relations
6.2.2 Stress-Strain Relations and Stress Resultants
6.2.3 Energy Functions
6.2.4 Governing Equations and Boundary Conditions
6.3 Vibration of Laminated Closed Conical Shells
6.3.1 Convergence Studies and Result Verification
6.3.2 Laminated Closed Conical Shells with General Boundary Conditions.
6.4 Vibration of Laminated Open Conical Shells
6.4.1 Convergence Studies and Result Verification
6.4.2 Laminated Open Conical Shells with General Boundary Conditions.
7 Spherical Shells
7.1 Fundamental Equations of Thin Laminated
……
8 Shallow Shells
References and Further Reading2100433B

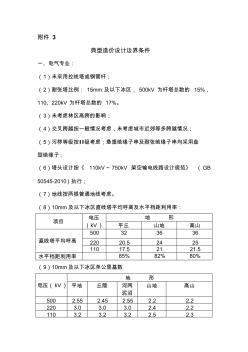 典型造价设计边界条件(V1.0版)
典型造价设计边界条件(V1.0版)

 考虑弹性隔板边界条件的柱形封闭腔结构-声耦合分析
考虑弹性隔板边界条件的柱形封闭腔结构-声耦合分析