平行线分线段成比例定理
平行线分线段成比例定理指的是两条直线被一组平行线所截,截得的对应线段的长度成比例。推论:平行于三角形一边的直线,截其他两边(或两边延长线)所得的对应线段成比例。
-

选择特殊符号
选择搜索类型
请输入搜索
平行线分线段成比例定理指的是两条直线被一组平行线所截,截得的对应线段的长度成比例。推论:平行于三角形一边的直线,截其他两边(或两边延长线)所得的对应线段成比例。

设三条平行线与直线1交于A、B、C三点,与直线2交于D、E、F三点。
连结AE、BD、BF、CE
根据平行线的性质可得S△ABE=S△DBE, S△BCE=S△BEF
∴S△ABE/S△CBE=S△DBE/S△BFE
根据不同底等高三角形面积比等于底的比可得:
AB/BC=DE/EF
由更比性质、等比性质得:
AB/DE=BC/EF=(AB+BC)/(DE+EF)=AC/DF
过一点的一线束被平行线截得的对应线段成比例。
平行于三角形一边的直线截其它两边(或两边的延长线)所得对应线段成比例。
平行于三角形一边,并且和其他两边相交的直线,所截得的三角形的三边与原三角形的三边对应成比例。
平行线分线段成比例定理:三条平行线截两条直线,所得对应线段成比例。推广:过一点的一线束被平行线截得的对应线段成比例。定理推论:①平行于三角形一边的直线截其它两边(或两边的延长线)所得对应线段成比例。②平行于三角形一边,并且和其他两边相交的直线,所截得的三角形的三边与原三角形的三边对应成比例。证明思路:该定理是用举例的方法引入的,没有给出证明,严格的证明要用到我们还未学到的知识,通过举例证明,让同学们承认这个定理就可以了,重要的是要求同学们正确地使用它(用相似三角形可以证明它,在这里要用到平移和设三条平行线与直线1交于A、B、C三点,与直线2交于D、E、F三点法1:过A作平行线的垂线交另两条平行线于M、N,过D作平行线的垂线交另两条平行线于P、Q,则四边形AMPD、ANQD均为矩形。AM=DP,AN=DQAB=AM/cosA,AC=AN/cosA,∴AB/AC=AM/ANDE=DP/cosD,DF=DQ/cosD,∴DE/DF=DP/DQ又∵AM=DP,AN=DQ,∴AB/AC=DE/DF根据比例的性质:AB/(AC-AB)=DE/(DF-DE)∴AB/BC=DE/EF法2:连结AE、BD、BF、CE根据平行线的性质可得S△ABE=S△DBE, S△BCE=S△BEF∴S△ABE/S△CBE=S△DBE/S△BFE根据不同底等高三角形面积比等于底的比可得:AB/BC=DE/EF由更比性质、等比性质得:AB/DE=BC/EF=(AB+BC)/(DE+EF)=AC/DF三条平行线截两条直线,所得对应线段成比例。这一定理被称为"平行线分线段成比例定理"。
如图,因为AD∥BE∥CF,
所以
AB:BC=DE:EF;
AB:AC=DE:DF;
BC:AC=EF:DF。
也可以说AB:DE=BC:EF;
AB:DE=AC:DF;
BC:EF=AC:DF。
上述图样只是平行线分线段的一种特殊情况。事实上,直线AC和直线DF可以在平行线之间相交,同样有定理成立。

 RVB平行线、RVS交织线、RXS紫花线、
RVB平行线、RVS交织线、RXS紫花线、
RVB平行线、RVS交织线、RXS紫花线、
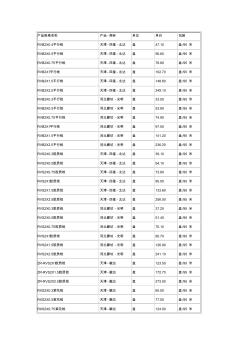
产品规格名称 产地 -商标 单位 单价 包装 RVB2X0.4平行线 天津 -四星 -北达 盘 47.10 盘 /95 米 RVB2X0.5平行线 天津 -四星 -北达 盘 56.60 盘 /95 米 RVB2X0.75平行线 天津 -四星 -北达 盘 78.80 盘 /95 米 RVB2X1平行线 天津 -四星 -北达 盘 102.70 盘 /95 米 RVB2X1.5平行线 天津 -四星 -北达 盘 148.60 盘 /95 米 RVB2X2.5平行线 天津 -四星 -北达 盘 249.10 盘 /95 米 RVB2X0.3平行线 河北廊坊 -光明 盘 33.50 盘 /95 米 RVB2X0.5平行线 河北廊坊 -光明 盘 53.80 盘 /95 米 RVB2X0.75平行线 河北廊坊 -光明 盘 74.90 盘 /95 米 RVB2X1平行线 河北廊坊 -光明 盘 97.50 盘

 垂线与平行线练习教学设计 (2)
垂线与平行线练习教学设计 (2)
垂线与平行线练习教学设计 (2)
垂线与平行线练习教学设计 科 目 数学 年 级 四 教 材 第 95页 课 题 垂线与平行线练习 课 时 2 教学目标 1.进一步巩固对垂线和平行线的认识, 能正确把握平面上两条直线的位置 关系。 2.进一步巩固对点到直线距离的认识, 能过直线上或直线外一点画已知直 线的垂线,会画已知直线的平行线。 教 学 重点、难点 重点:在动手操作中进一步巩固对垂线和平行线的认识,对点到直线距 离的认识。 教具准备 直尺、三角尺、量角器 教 学 过 程 备 课 一、揭题。 二、完成练习十五第 8—13题。 1. 练习十五第 8 题。 学生独立完成测量。 反馈,说说量角时需要注意的问题。 2. 练习十五第 9 题。 学生独立完成判断。 反馈,说明理由。 交流明确:同一平面内的两条直线,要么相交,要么平行; 相交的两条直线中,如果相交成直角,这两条直线就互相垂直, 否则,两条直线就不互相垂直。 3. 练
香农定理用来求信道的最大传输速率,即信道容量,当通过信道的信号速率超过香农定理的信道容量时,误码率显著提高,信息质量严重下降。需要指出的是这里的信道容量只是理论上可以达到的极限,实际如何达到,该定理不能说明。
从圆外一点引圆的两条割线,这一点到每条割线与圆交点的距离的积相等。
从圆外一点P引两条割线与圆分别交于C,B,D,E,则有 PC·PB=PD·PE。如下图所示。 (PA是切线)
Secant Theorem
割线定理为圆幂定理之一(切割线定理推论),其他二为:
切割线定理
相交弦定理
如图直线PB和PE是自点P引的⊙O的两条割线,则PC·PB=PD·PE.
证明:连接CE、DB
∵∠E和∠B都对弧CD
∴由圆周角定理,得 ∠E=∠B
又∵∠EPC=∠BPD
∴△PCE∽△PDB
∴PC:PD=PE:PB, 也就是PC·PB=PD·PE.
割线定理与相交弦定理,切割线定理通称为圆幂定理。

相交弦定理、切割线定理以及它们的推论统称为圆幂定理。一般用于求线段长度。