最大完备子图C 算法示例文献

 最大允许玻璃面积(附录(C))
最大允许玻璃面积(附录(C))
最大允许玻璃面积(附录(C))
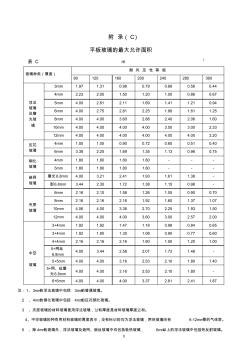
0 附 录( C) 平板玻璃的最大允许面积 表 C m 2 玻璃种类(厚度) 耐 风 压 性 等 级 80 120 160 200 240 280 360 浮法 玻璃 及磨 光玻 璃 3mm 1.97 1.31 0.98 0.79 0.66 0.56 0.44 4mm 2.23 2.00 1.50 1.20 1.00 0.86 0.67 5mm 4.00 2.81 2.11 1.69 1.41 1.21 0.94 6mm 4.00 2.75 2.81 2.25 1.88 1.61 1.25 8mm 4.00 4.00 3.60 2.88 2.40 2.06 1.60 10mm 4.00 4.00 4.00 4.00 3.50 3.00 2.33 1

 “重庆造”铝板装备最大射电望远镜
“重庆造”铝板装备最大射电望远镜
“重庆造”铝板装备最大射电望远镜
8月14日从西南铝业集团获悉,西南铝为我国正在研发制造的全球最大射电望远镜(FAST工程)提供的首批铝材,已于近日交付使用。在这台有着全球第一“天眼”之称的射电望远镜上,约30个足球场面积大小的反射面面板及铝板结构件,全部由西南铝供货,这也是我国铝加工企业在天文射电领域的“首秀”。