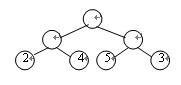
在数据通讯中,经常需要将传送的文字转换成由二进制字符0,1组成的二进制串,我们称之为编码。例如,假设要传送的电文为ABACCDA,电文中只含有A,B,C,D四种字符,若这四种字符采用表7.3 (a)所示的编码,则电文的代码为000010000100100111 000,长度为21。在传送电文时,我们总是希望传送时间尽可能短,这就要求电文代码尽可能短,显然,这种编码方案产生的电文代码不够短。表7.3 (b)所示为另一种编码方案,用此编码对上述电文进行编码所建立的代码为00010010101100,长度为14。在这种编码方案中,四种字符的编码均为两位,是一种等长编码。如果在编码时考虑字符出现的频率,让出现频率高的字符采用尽可能短的编码,出现频率低的字符采用稍长的编码,构造一种不等长编码,则电文的代码就可能更短。如当字符A,B,C,D采用表7.3 (c)所示的编码时,上述电文的代码为0110010101110,长度仅为13。
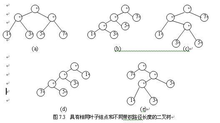
表a、表b、表c、表d(从下图的上下顺序依次列出)
表3 字符的四种不同的编码方案
哈夫曼树可用于构造使电文的编码总长最短的编码方案。具体做法如下:设需要编码的字符集合为{d1,d2,…,dn},它们在电文中出现的次数或频率集合为{w1,w2,…,wn},以d1,d2,…,dn作为叶结点,w1,w2,…,wn作为它们的权值,构造一棵哈夫曼树,规定哈夫曼树中的左分支代表0,右分支代表1,则从根结点到每个叶结点所经过的路径分支组成的0和1的序列便为该结点对应字符的编码,我们称之为哈夫曼编码。
在哈夫曼编码树中,树的带权路径长度的含义是各个字符的码长与其出现次数的乘积之和,也就是电文的代码总长,所以采用哈夫曼树构造的编码是一种能使电文代码总长最短的不等长编码。
在建立不等长编码时,必须使任何一个字符的编码都不是另一个字符编码的前缀,这样才能保证译码的唯一性。例如表7.3 (d)的编码方案,字符A的编码01是字符B的编码010的前缀部分,这样对于代码串0101001,既是AAC的代码,也是ABD和BDA的代码,因此,这样的编码不能保证译码的唯一性,我们称之为具有二义性的译码。
然而,采用哈夫曼树进行编码,则不会产生上述二义性问题。因为,在哈夫曼树中,每个字符结点都是叶结点,它们不可能在根结点到其它字符结点的路径上,所以一个字符的哈夫曼编码不可能是另一个字符的哈夫曼编码的前缀,从而保证了译码的非二义性。
下面讨论实现哈夫曼编码的算法。实现哈夫曼编码的算法可分为两大部分:
(1)构造哈夫曼树;
(2)在哈夫曼树上求叶结点的编码。
求哈夫曼编码,实质上就是在已建立的哈夫曼树中,从叶结点开始,沿结点的双亲链域回退到根结点,每回退一步,就走过了哈夫曼树的一个分支,从而得到一位哈夫曼码值,由于一个字符的哈夫曼编码是从根结点到相应叶结点所经过的路径上各分支所组成的0,1序列,因此先得到的分支代码为所求编码的低位码,后得到的分支代码为所求编码的高位码。我们可以设置一结构数组HuffCode用来存放各字符的哈夫曼编码信息,数组元素的结构如下:
其中,分量bit为一维数组,用来保存字符的哈夫曼编码,start表示该编码在数组bit中的开始位置。所以,对于第i个字符,它的哈夫曼编码存放在HuffCode.bit中的从HuffCode.start到n的分量上。
求哈夫曼编码程序段
const Maxleaf=128; {定义最多叶结点数}
MaxNode=255; {定义最大结点数}
MaxBit=10; {定义哈夫曼编码的最大长度}
type HCodeType =record
bit: array[0..MaxBit] of integer;
start: integer;
end;
……
procedure HaffmanCode ; {生成哈夫曼编码}
var HuffNode: array[0..MaxNode] of HCodeType;
HuffCode: array[0..MaxLeaf] of HcodeType;
cd : HcodeType ;
i,j, c,p: integer ;
begin
HuffmanTree (HuffNode ); {建立哈夫曼树}
for i:=0 to n-1 do {求每个叶子结点的哈夫曼编码}
begin
cd.start:=n-1; c:=i;
p:=HuffNode[c].parent;
while p<>0 do {由叶结点向上直到树根}
if HuffNode
.lchild=c then cd.bit[cd.start]:=0
else cd.bit[cd.start]:=1;
dec (cd.start); c:=p;
p:=HuffNode[c].parent;
end;
for j:=cd.start 1 to n-1 do {保存求出的每个叶结点的哈夫曼编码和编码的起始位}
begin
HuffCode.bit[j]:=cd.bit[j];
HuffCode.start=cd.start;
end;
for i:=0 to n-1 do {输出每个叶子结点的哈夫曼编码}
begin
for j:=HuffCode.start 1 to n-1 do write(HuffCode.bit[j]:10);
writeln;
end;
end;