望海岛
今有望海岛,立两表,齐高三丈,前后相去千步,令后表与前表三相直。从前表却行一百二十三步,人目着地取望岛峰,与表末三合。从后表却行一百二十七步,人目着地取望岛峰,亦与表末三合。问岛高及去表各几何? 答曰:岛高四里五十五步;去表一百二里一百五十步。 术曰:以表高乘表间为实;相多为法,除之。所得加表高,即得岛高。求前表去岛远近者:以前表却行乘表间为实;相多为法。除之,得岛去表里数。
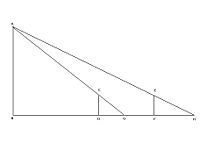
望海岛二次测量示意图
由于前表去岛的距离不能直接测量,刘徽用同样高度的表杆前后测量,表杆与地面垂直,人眼贴地,望表杆顶和岛上山顶对齐,这时测得人眼和前表杆的水平距离叫"前表却行"DF=123步;再将表杆往后移动,两彪杆间距称为"表间"=1000步,依法测出"后表却行"FH=127步。
表高 =CD, 前表却行=DG 后表却行=FH 相多=FH-DG 表间=DF 岛高=AB 前表去岛远近=BD
依法得岛高AB=CDxDF/(FH-DG)+CD
前表去岛远近BD=DGxDF/(FH-DG)
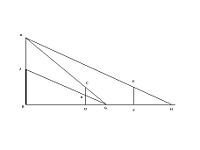
松生山上三次测量示意图
望松生山上
今有望松生山上,不知高下。立两表齐,高二丈,前后相去五十步,令后表与前表三相直。从前表却行七步四尺,薄地遥望松末,与表端三合。又望松本,入表二尺八寸。复从后表却行八步五尺,薄地遥望松末,亦与表端三合。问松高及山去表各几何? 答曰:松高一十二丈二尺八寸;山去表一里二十八步、七分步之四。术曰:以入表乘表间为实。相多为法,除之。加入表,即得松高。求表去山远近者:置表间,以前表却行乘之为实。相多为法,除之,得山去表。
CD EF 表示前后两支表杆,前表杆有刻度,用作两次测量,第一次从G点瞄准A、C两点成直线,第二次从G点校准树根J,读出前表杆上度数(入表)。
表高 =CD=2丈 前表却行=DG=7步4尺 后表却行=FH=8步5尺 相多=FH-DG 表间=DF=50步 松高=AJ 前表去山远近=BD 入表=CK=二尺八寸
松高=AJ=CK x DF/(FH-DG)+CK 前表去山远近=BD=DF x DG/(FH-DG)
南望方邑
今有南望方邑,不知大小。立两表东、西去六丈,齐人目,以索连之。令东表与邑东南隅及东北隅三相直。当东表之北却行五步,遥望邑西北隅,入索东端二丈二尺六寸半。又却北行去表一十三步二尺,遥望邑西北隅,适与西表相三合。问邑方及邑去表各几何? 答曰:邑方三里四十三步、四分步之三;邑去表四里四十五步。 术曰:以入索乘后去表,以两表相去除之,所得为景差;以前去表减之,不尽以为法。置后去表,以前去表减之,馀以乘入索为实。实如法而一,得邑方。求去表远近者:置后去表,以景差减之,馀以乘前去表为实。实如法而一,得邑去表。
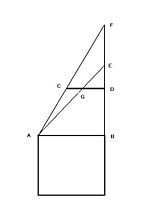
由于待测的方城宽度AB,在东西方向,与地面平行,因此两支在C点D点插入地面与地面垂直的表杆,在此不用作直接测量,测量是依靠一根拴在C、D两根垂直表杆中间的一条水平测量绳索CD完成的。此题中一根水平测量绳作两次测量用。
望深谷
今有望深谷,偃矩岸上,令勾高六尺。从勾端望谷底,入下股九尺一寸。又设重矩于上,其矩间相去三丈。更从勾端望谷底,入上股八尺五寸。问谷深几何?答曰:四十一丈九尺。术曰:置矩间,以上股乘之,为实。上、下股相减,馀为法,除之。所得以勾高减之,即得谷深。
登山望楼
今有登山望楼,楼在平地。偃矩山上,令句高六尺。从句端斜望楼足,入下股一丈二尺。又设重矩于上,令其间相去三丈。更从句端斜望楼足,入上股一丈一尺四寸。又立小表于入股之会,复从句端斜望楼岑端,入小表八寸。问楼高几何? 答曰:八丈。 术曰:上下股相减,馀为法;置矩闲,以下股乘之,如句高而一。所得,以入小表乘之,为实。实如法而一,即是楼高。
南望波口
今有东南望波口,立两表南、北相去九丈,以索薄地连之。当北表之西却行去表六丈,薄地遥望波口南岸,入索北端四丈二寸。以望北岸,入前所望表里一丈二尺。又却后行1去表一十三丈五尺。薄地遥望波口南岸,与南表三合。问波口广几何?答曰:一里二百步。 术曰:以后去表乘入索,如表相去而一。所得,以前去表减之,馀以为法;复以前去表减后去表,馀以乘入所望表里为实,实如法而一,得波口广。
此题中一根水平测量绳,作三次测量用
今有望清渊,渊下有白石。偃矩岸上,令句高三尺。斜望水岸,入下股四尺五寸。望白石,入下股二尺四寸。又设重矩于上,其间相去四尺。更从句端斜望水岸,入上股四尺。以望白石,入上股二尺二寸。问水深几何? 答曰:一丈二尺。 术曰:置望水上下股相减,馀以乘望石上股为上率。又以望石上下股相减,馀以乘望水上股为下率。两率相减,馀以乘矩间为实;以二差相乘为法。实如法而一,得水深。又术:列望水上下股及望石上下股,相减,馀为法。以望石下股减望水下股,馀以乘矩间为实,实如法而一,得水深。
A标志水岸,S标志白石,C标志岸边;句是古代测量用具之一,有两个边成直角(如今三角板):使用时句的一边务必与地面垂直。此题用两个句,一个在C,一个在D,各测量水岸和水底白石。此题用四次测望术。
登山望津
今有登山望津,津在山南。偃矩山上,令句高一丈二尺。从句端斜望津南岸,入下股二丈三尺一寸。又望津北岸,入前望股里一丈八寸。更登高岩北,却行二十二步,上登五十一步,偃矩山上。更从句端斜望津南岸,入上股二丈二尺。问津广几何? 答曰:二里一百二步。 术曰:以句高乘下股,如上股而一。所得以句高减之,馀为法;置北行,以句高乘之,如上股而一。所得以减上登,馀以乘入股里为实。实 如法而一,即得津广。
登山临邑
今有登山临邑,邑在山南。偃矩山上,令勾高三尺五寸。令勾端与邑东南隅及东北隅三相直。从勾端遥望东北隅,入下股一丈二尺。又施横勾于入股之会,从立勾端望西北隅,入横勾五尺。望东南隅,入下股一丈八尺。又设重矩于上,令矩间相去四丈。更从立勾端望东南隅,入上股一丈七尺五寸。问邑广长各几何? 答曰:南北长一里一百步;东西广一里三十三步、少半步。术曰:以勾高乘东南隅入下股,如上股而一,所得减勾高,馀为法;以东北隅下股减东南隅下股,馀以乘矩间为实。实如法而一,得邑南北长也。求邑广:以入横勾乘矩间为实。实如法而一,即得邑东西广。
此题用四次测望术
注:《海岛算经》共九问。从题目文字可知所有计算都是用筹算进行的。"为实"指作为一个分数的分子,"为法"指作为分数的分母。所用的长度单位有里、丈、步、尺、寸;1里=180丈=1800尺;1丈=10尺:1步=6尺,1尺=10寸。
-