选择特殊符号

Ф δ ° × # Ⅱ Ⅲ ½ ¼

选择搜索类型

市场价信息价参考价询价供应商云知资讯文库百科

热门搜索

造价通

请输入搜索

首页 > 百科 > 建设工程百科

简化测度

简化测度（reduced measure）是一般位势论中简化函数的类似物，简化测度也是超过测度。

简化测度基本信息

中文名简化测度
外文名reduced measure
适用范围数理科学

简化测度性质

也是超过测度， 且在G上 。 超过测度的里斯分解式 满足 。若G是相对紧的开集，则 是一个位势。 特别地， 是一个位势，所以存在惟一的σ(G)∈G(χ)，使得 。

简化测度造价信息

市场价
信息价
询价

球墨铸铁双盘简化短管

规格型号：
DN600/DN600
价格行情：
材料单位：
个
材料品牌：
材料税率：
13%
供应商：
泽州县世纪球墨铸造有限公司保定销售处
报价时间：
2022-12-07

查看价格

M随心配镜柜

规格型号：
K-15512T-NL/NR-NA 489mm简化版-左开门/右开门
价格行情：
材料单位：
个
材料品牌：
材料税率：
13%
供应商：
科勒(中国)投资有限公司
报价时间：
2022-12-07

查看价格

浴室家具

规格型号：
15512T-NR-NA 20寸M随心配镜柜(简化版右开门)/15512T-NR-NA
价格行情：
材料单位：
套
材料品牌：
科勒
材料税率：
13%
供应商：
北京建贸新科建材有限公司
报价时间：
2022-12-07

查看价格

远程控制器

规格型号：
产品号:537100-B21 针对1路服务器的简化标准版适用范围:ML110G7/DL120G7
价格行情：
材料单位：
套
材料品牌：
材料税率：
13%
供应商：
广州昊群计算机科技有限公司
报价时间：
2022-12-07

查看价格

48口接入交换机

规格型号：
包转发速率:≥17Mpps;交换容量:≥64Gbps;支持百兆电端口≥48个千兆电口≥2个千兆光口≥2个;为简化管理要求设备支持堆叠;
价格行情：
材料单位：
个
材料品牌：
华为
材料税率：
13%
供应商：
深圳市众盈创达科技有限公司
报价时间：
2022-12-07

查看价格

承插简化短管

规格型号：
DN100
需求量：
1个
报价数：
2
材料品牌：
材料档次：
费用说明：
不含税费 | 不含运费
询价时间：
2015-03-26

查看价格

双盘简化短管DN400

规格型号：
球墨铸铁
需求量：
1个
报价数：
1
材料品牌：
材料档次：
中档
费用说明：
含税费 | 含运费
询价时间：
2015-06-15

查看价格

双盘简化短管DN80

规格型号：
球墨铸铁
需求量：
1个
报价数：
1
材料品牌：
材料档次：
中档
费用说明：
含税费 | 含运费
询价时间：
2015-06-15

查看价格

铸铁盘插简化短管

规格型号：
DN150
需求量：
1个
报价数：
2
材料品牌：
材料档次：
费用说明：
不含税费 | 不含运费
询价时间：
2015-03-26

查看价格

自动化监控系统-NH3-N测度仪

规格型号：
0-320mg/L(详见自控图)
需求量：
1套
报价数：
1
材料品牌：
材料档次：
高档
费用说明：
含税费 | 含运费
询价时间：
2021-08-26

查看价格

简化测度简化函数

简化函数是在一个子集上不小于一个给定函数的一族函数的下确界。 设Φ是一族从Ω到[0, ∞]的下半连续的函数u所组成的凸锥（必要时设 ∞∈Φ），f为E(E⊂Ω)到[0, ∞]的函数，令 =inf{u(x)|u∈Φ且u|E≥f}（对空集∅，令 =0)，称之为f到E的简化函数。2100433B

简化测度简介

简化测度是一般位势论中简化函数的类似物。 设G是开集，ξ是超过测度，那么测度 =inf{μ|μ是超过测度且在G上μ≥ξ}称为ξ在G上的简化测度。

简化测度常见问题

简化预算问题

如果那样的话造价人员还有存在的意思么? 计算机都能做了，人的价值就没了当然未来的事情很可能会发展到那一块
标高设置如何简化？

没有复制前不要修改梁的标高，让梁标高按楼层，复制后也是按楼层的
简化多栋同类型房屋计算。

简化多栋同类型房屋计算。目前做一个项目，10多栋房子，有很多相似的地方，结构上：砖混和底框均有。户型：abc三种。目前已经做了几栋了，想利用下现成的模板。我的回答：建议直接做ABC三种户型进行汇总计...

简化测度文献

验针灵敏度测度记录表

验针灵敏度测度记录表

验针灵敏度测度记录表

格式：pdf

大小：31KB

页数： 2页

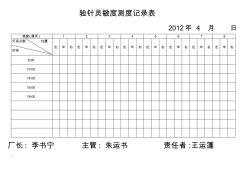
验针灵敏度测度记录表 2012年 4 月日高度 (厘米 ) 1 2 3 4 5 6 7 8 灯亮点数位置时间左中右左中右左中右左中右左中右左中右左中右左中右 8:00 10:00 14:00 16:00 19:00 厂长 : 李书宁主管 : 朱运书责任者 :王运蓬验针灵敏度测度记录表 2012年 4 月日高度 (厘米 ) 1 2 3 4 5 6 7 8 灯亮点数位置时间左中右左中右左中右左中右左中右左中右左中右左中右 8:00 10:00 14:00 16:00 19:00 厂长 : 李书宁主管 : 朱运书责任者 :王运蓬

在线阅读立即下载

挤压筒的简化设计

挤压筒的简化设计

挤压筒的简化设计

格式：pdf

大小：31KB

页数： 3页

挤压筒是铜材生产的关键模具之一,工作时需要承受高温、高压、高摩擦的作用。本文从挤压筒的结构、选材及强度校核几方面,通过分析计算,提出了挤压筒简化计算的原理,在实际使用中取得了显著的经济效益。

在线阅读立即下载

测度问题简介

测度问题是测度论中的著名问题。 对于直线而论，人们总希望直线上某个测度，关于它可测的集合越多越好。可测集多，意味着可测函数多，从而可积函数也多。对于平面或高维空间的情形也是这样。 所谓测度问题，就是（直线上）是否存在具有下列性质的测度： 1、具有可列可加性； 2、（直线上的）所有子集都可测； 3、具有平移不变性； 4、[0,1]的测度是1。

测度问题发展

测度问题是勒贝格(Lebesgue,H.L.)于1904年提出的，这个问题已经解决，结论如下：去掉测度论性质2,3,4中任何一条，容易举例说明满足其余三条的测度是存在的。性质1,2,3,4全都满足的测度是不存在的，特别地，直线上必存在不是勒贝格可测的集，这首先是由维塔利(Vitali,G.)于1905年指出的。

测度问题性质

如果将测度问题性质1换成1'：具有有限可加性，则满足1',2,3,4的测度是存在的，但不惟一，这就是著名的巴拿赫定理。 对于空间Rⁿ(n≥2)，则有结论： 当n=2时，满足1',2,3,4的测度是存在的。 当n≥3时，满足1',2,3,4的测度是不存在的。 这个问题是由豪斯多夫(Hausdorff,F.)于1914年提出并于1923年解决的。 2100433B

相关推荐

相关百科
相关知识
相关专栏

免费服务热线: 400-888-9639