秩统计量文献

 照明统计量
照明统计量
照明统计量
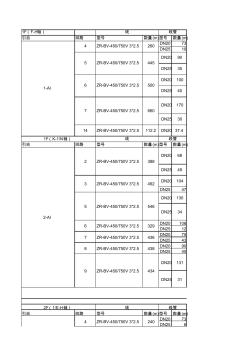
1F(F-H轴) 引自 回路 型号 数量 (m)型号 数量 (m) DN20 73 DN25 10 引自 回路 型号 数量 (m)型号 数量 (m) DN25 47 DN20 106 DN25 12 DN20 75 DN25 43 DN20 90 DN25 40 引自 回路 型号 数量 (m)型号 数量 (m) DN20 73 DN25 6 436 2F(1/E-H轴) 线 线管 9 2-Al ZR-BV-450/750V 3*2.5 434 DN20 37.4 2 ZR-BV-450/750V 3*2.5 388 DN20 68 1F(K-1/N轴) 线 线管 DN25 49 1-Al 6 ZR-BV-450/750V 3*2.5 500 DN20 100 DN25 40 7 ZR-BV-450/750V 3*2.5 660 DN20 170 8 ZR-BV-450/750V 3*2.5

 施工项目统计、计量管理
施工项目统计、计量管理
施工项目统计、计量管理
施工项目统计、计量管理——6.1 一般要求 6.2 报表编制原则 6.3 工程统计管理 6.4 工程计量管理 6.5 对作业队统计、计量资料的要求 …… 附表: 项目经理部建安工作量实际完成情况统计台帐 项目经理部实物工程量实际完成情况统...