角平分线长公式第二形式

角平分线长公式公式 三角形ABC的角平分线为AD，D在CB上。则 角平分线长公式推导过程 证明。如图3，延长AC到E，使CE=CD，连接DE，则AE=AC CD， 。在AB边上取点F，使BF=BD，连接DF，则AF=AB－BD，∠BDF=∠BFD。则 即 又 则 于是 ，便有 ，故 又 由角平分线定理得 即 代入①中得 证毕。

查看详情

角平分线长公式造价信息

市场价
信息价
询价

控制分线

规格型号：
RVV4*0.5
价格行情：
材料单位：
m
材料品牌：
材料税率：
13%
供应商：
深圳市中联泰电子有限公司广西办事处
报价时间：
2022-12-08

查看价格

河长公示牌

规格型号：
尺寸:2300×2300
价格行情：
材料单位：
个
材料品牌：
材料税率：
13%
供应商：
广州千艺五金制品有限公司
报价时间：
2022-12-08

查看价格

三角形焊线

规格型号：
TR-7mm
价格行情：
材料单位：
m
材料品牌：
材料税率：
13%
供应商：
重庆好师傅新型建材有限公司
报价时间：
2022-12-08

查看价格

分线箱

规格型号：
2500A/4P
价格行情：
材料单位：
台
材料品牌：
材料税率：
13%
供应商：
深圳邦顿五金建材有限公司
报价时间：
2022-12-08

查看价格

分线箱

规格型号：
品种:分线箱;型号:ZH1304/20;规格:20线;类型:专业;外形尺寸(mm):240×170×55(mm);
价格行情：
材料单位：
台
材料品牌：
众海
材料税率：
13%
供应商：
山东众海智能科技有限公司
报价时间：
2022-12-08

查看价格

查看详情

联合角咬口机

规格型号：
YZL-12B
价格行情：
材料单位：
个
材料税率：
地区时间：
深圳市2007年8月信息价
所属行业：
建筑工程
备注说明：

查看价格

联合角咬口机

规格型号：
YZL-16W
价格行情：
材料单位：
个
材料税率：
地区时间：
深圳市2007年8月信息价
所属行业：
建筑工程
备注说明：

查看价格

联合角咬口机

规格型号：
YZL-16W
价格行情：
材料单位：
个
材料税率：
地区时间：
深圳市2007年1月信息价
所属行业：
建筑工程
备注说明：

查看价格

联合角咬口机

规格型号：
YZL-16W
价格行情：
材料单位：
个
材料税率：
地区时间：
深圳市2006年6月信息价
所属行业：
建筑工程
备注说明：

查看价格

联合角咬口机

规格型号：
YZL-12B
价格行情：
材料单位：
个
材料税率：
地区时间：
深圳市2006年5月信息价
所属行业：
建筑工程
备注说明：

查看价格

查看详情

河长公示标识

规格型号：
1.类型:河长公示标识2.材质、规格尺寸:5mm厚中空钢板刷灰色氟碳漆,1530×2200×50mm;5厚50x50方钢面刷紫檀色仿木氟碳漆;名称信息、logo、辅助图案等3.不包含基础4.详见图纸
需求量：
18块
报价数：
3
材料品牌：
无
材料档次：
中档
费用说明：
不含税费 | 含运费
询价时间：
2021-09-15

查看价格

光纤分线箱

规格型号：
满足TIA/EIA 以及 ISO/IEC 6类/E级规格要求. 多股铜芯绞合的软跳线设计,跳线长度3米.
需求量：
1台
报价数：
2
材料品牌：
材料档次：
费用说明：
不含税费 | 不含运费
询价时间：
2016-10-20

查看价格

河长公示标识

规格型号：
详见图纸大样,不含基础
需求量：
2组
报价数：
3
材料品牌：
无
材料档次：
中档
费用说明：
不含税费 | 含运费
询价时间：
2022-06-30

查看价格

数据统计公式配置

规格型号：
配置计算量统计公式,分单个泵房和高中低区泵房(泵房的综合配水和供水单耗单耗,水泵的综合和配水单耗,消毒供水单耗,总用电量,水泵,消毒,照明,空调,除湿机,插座的用电量,供水量和平均压力)的小时数据和天数据总共48个相关公司配置和数据检查核对等.每个泵房按照中级软件工程师0.6人天计算.
需求量：
99套
报价数：
3
材料品牌：
材料档次：
中档
费用说明：
含税费 | 含运费
询价时间：
2022-03-27

查看价格

二线长途板

规格型号：
RGT-07人工交换机单板8路磁石中继用户用于引接磁石用户线路
需求量：
16套
报价数：
1
材料品牌：
上海新殿光
材料档次：
费用说明：
不含税费 | 不含运费
询价时间：
2015-12-03

查看价格

查看详情

角平分线长公式第三形式

角平分线长公式公式 △ABC中，角平分线 角平分线长公式推导过程 证明。如图4，设AB、AC、AD长a、b、f。易知 即 于是 证毕。 外角平分线长公式 公式 下面不加证明地给出公式。在△ABC中，∠A的外角平分线记为 ，∠B的角平分线记为 ，∠C的角平分线记为 ，三边边长为a、b、c，则 2100433B

查看详情

角平分线长公式第一形式

角平分线长公式公式 在△ABC中，∠A的角平分线记为 ，∠B的角平分线记为 ，∠C的角平分线记为 ，三边边长为a、b、c，则 其中p是半周长。 角平分线长公式推导过程 证明。法一。如图1，我们先证明 。 由角平分线定理可得 ，并注意到 ，消去 ，化简得 。 由余弦定理， ， 把 和 的表达式代入（1）中， 即 设 ，那么上式可以写成 于是 其他角平分线长度同理可证。 证毕。 提要。法二。运用斯特瓦尔特定理，可得证明。

查看详情

角平分线长公式常见问题

证明三角形内外角平分线定理

三角形外角定理证明过程; http://zhidao.baidu.com/question/59352008.html?si=1三角形内角定理:(1)角的平分线是到角的两边距离相等的所有点的集合．∠A...
球弧长公式

S=a*3.14*r/180 s为弧长 a为弧长s所对应的圆心角 r为半径
请列斜长公式

你好：150/200=tg36.87 净长=你所指出长度的水平长度/cos36.87 用三角函数的关系计算最简单了。

查看详情

角平分线长公式文献

鲁教版六年级下册线段中点与角平分线练习(无答案)

格式：pdf

大小：88KB

页数： 3页

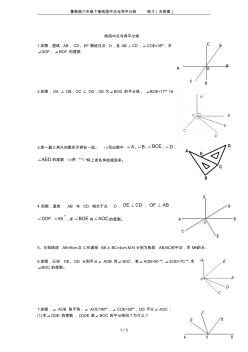
鲁教版六年级下册线段中点与角平分线练习（无答案） 1 / 3 线段中点与角平分线 1.如图，直线 AB、CD、EF 都经过点 O，且 AB⊥CD，∠COE=35°，求 ∠DOF、∠BOF 的度数． 2.如图，OA 丄 OB，OC 丄 OD，OE 为∠BOD 的平分线， ∠BOE=17° 18 3.把一副三角尺如图所示拼在一起。 ⑴写出图中 A、 B、 BCE、 D、 AED的度数；⑵用 “ ”将上述各角连接起来。 4.如图，直线 AB 与 CD 相交于点 O， CDOE ， ABOF ， 65DOF ，求 BOE与 AOC的度数。 5、已知线段 AB=6cm,点 C在直线 AB上,BC=4cm,M,N分别为线段 AB,BC的中点 ,求 MN的长 . 6.如图，已知 OE、OD 分别平分∠ AOB 和∠ BOC，若∠ AOB=90°，∠EOD=70°，求 ∠BOC 的度数。 7.如图，

在线阅读立即下载

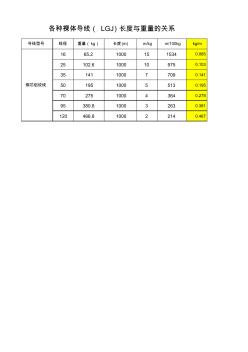
LGJ导线长度与重量关系

格式：pdf

大小：88KB

页数： 1页

导线型号线径重量（ kg）长度 (m) m/kg m/100kg kg/m 16 65.2 1000 15 1534 0.065 25 102.6 1000 10 975 0.103 35 141 1000 7 709 0.141 50 195 1000 5 513 0.195 70 275 1000 4 364 0.275 95 380.8 1000 3 263 0.381 120 466.8 1000 2 214 0.467 各种裸体导线（ LGJ）长度与重量的关系钢芯铝绞线

在线阅读立即下载

角平分线定理验证推导

已知，如图4，AM为△ABC的角平分线，求证: 角平分线定理面积法 由三角形面积公式，得 S△ABM=(1/2)·AB·AM·sin∠BAM S△ACM=(1/2)·AC·AM·sin∠CAM ∵AM是∠BAC的角平分线 ∴∠BAM=∠CAM ∴sin∠BAM=sin∠CAM ∴S△ABM:S△ACM=AB:AC 根据：等高底共线，面积比=底长比 可得：S△ABM:S△ACM=MB:MC，则AB:AC=MB:MC 角平分线定理相似法 过C作CN∥AB，交AM的延长线于N ∵CN∥AB ∴∠ABC=∠BCN 又 ∠AMB=∠CMN ∴△ABM∽△NCM ∴AB:NC=BM:CM ∵AM是∠BAC的角平分线 ∴∠BAN=∠CAN 又 ∠BAN=∠ANC ∴∠CAN=∠ANC ∴AC=CN ∴AB:AC=MB:MC （过M作MN∥AB交AC于N也可证明） 角平分线定理正弦定理法 作△ABC的外接圆，AM交圆于D 由正弦定理，得 AB:sin∠AMB=MB:sin∠BAM, AC:sin∠AMC=MC:sin∠CAM ∵AM是∠BAC的角平分线 ∴∠BAM=∠CAM 又∠AMB ∠AMC=180° ∴sin∠BAM=sin∠CAM sin∠AMB=sin∠AMC ∴AB:AC=MB:MC

查看详情

角平分线性质定理证明

●三角形内角平分线分对边所成的两条线段，和两条邻边成比例. 即在三角形ABC中，当AD是顶角A的角平分线交底边于D时，BD/CD=AB/AC. 证明 : 如图，AD为△ABC的角平分线，过点D向边AB,AC分别引垂线DE,DF.则DE=DF. S△ABD:S△ACD=BD/CD 又因为S△ABD:S△ACD=[(1/2)AB×DE]:[(1/2)AC×DF]=AB:AC 所以BD/CD=AB/AC. 第一部分 1.角平分线可以得到两个相等的角。 角平分线，顾名思义，就是将角平分的射线。 如右图，若射线AD是角CAB的角平分线，则角CAD等于角BAD。 第二部分 2.角平分线线上的点到角两边的距离相等。 如右上图，若射线AD是∠CAB的角平分线，求证:CD=BD ∵∠DCA=∠DBA ∠CAD=∠BAD AD=AD ∴△ACD≌△ABD ∴CD=BD 第三部分 3.三角形的三条角平分线交于一点，称作三角形的内心。三角形的内心到三角形三边的距离相等。 这一条是第二条的引申，详细证明过程参照第二条和三角形内心。 第四部分 4.三角形一个角的平分线，这个角平分线其对边所成的两条线段与这个角的两邻边对应成比例。 如右下图，平面内任意一小于180度的∠MAN，AS平分∠MAN，直线BC分别交射线AM、AN、AS于B、C、D，求证:AB/BD=AC/CD: 作BE=BD交射线AS于E，如图1: ∵BE=BD， ∴∠BED=∠BDE， ∴∠AEB=∠ADC 又∵∠BAE=∠CAD, ∴△AEB∽△ADC, ∴AB/BE=AC/CD, 即AB/BD=AC/CD. 另外的情况， 如图2，直线BC交AS的反向延长线于D, 如图3，直线BC交AN的反向延长线于C; 此时，仍有AB/BD=AC/CD 证法与图1类似

查看详情

热门搜索

角平分线长公式

角平分线长公式基本信息

角平分线长公式第二形式

角平分线长公式公式

角平分线长公式推导过程

角平分线长公式造价信息

控制分线

河长公示牌

三角形焊线

分线箱

分线箱

联合角咬口机

联合角咬口机

联合角咬口机

联合角咬口机

联合角咬口机

河长公示标识

光纤分线箱

河长公示标识

数据统计公式配置

二线长途板

角平分线长公式第三形式

角平分线长公式公式

角平分线长公式推导过程

角平分线长公式第一形式

角平分线长公式公式

角平分线长公式推导过程

角平分线长公式常见问题

角平分线长公式文献

角平分线定理验证推导

角平分线定理面积法

角平分线定理相似法

角平分线定理正弦定理法

角平分线性质定理证明

第一部分

第二部分

第三部分

第四部分

角平分线定理应用例子

相关推荐