角平分线长公式造价信息

市场价
信息价
询价

三角形焊线

规格型号：
TR-7mm
价格行情：
材料单位：
m
材料品牌：
材料税率：
13%
供应商：
重庆好师傅新型建材有限公司
报价时间：
2022-12-08

查看价格

三角梅

规格型号：
高度55-75cm,冠幅45-65cm
价格行情：
材料单位：
株
材料品牌：
瀚艺
材料税率：
13%
供应商：
南宁瀚艺生态苗圃种植基地
报价时间：
2022-12-08

查看价格

三角梅

规格型号：
高度100-120cm,冠幅80-90cm
价格行情：
材料单位：
株
材料品牌：
瀚艺
材料税率：
13%
供应商：
南宁瀚艺生态苗圃种植基地
报价时间：
2022-12-08

查看价格

三角托架

规格型号：
1600A
价格行情：
材料单位：
副
材料品牌：
众联兴
材料税率：
13%
供应商：
众联兴电力科技有限公司
报价时间：
2022-12-08

查看价格

三角托架

规格型号：
630A
价格行情：
材料单位：
副
材料品牌：
众联兴
材料税率：
13%
供应商：
众联兴电力科技有限公司
报价时间：
2022-12-08

查看价格

查看详情

联合角咬口机

规格型号：
YZL-12B
价格行情：
材料单位：
个
材料税率：
地区时间：
深圳市2007年8月信息价
所属行业：
建筑工程
备注说明：

查看价格

联合角咬口机

规格型号：
YZL-16W
价格行情：
材料单位：
个
材料税率：
地区时间：
深圳市2007年8月信息价
所属行业：
建筑工程
备注说明：

查看价格

联合角咬口机

规格型号：
YZL-16W
价格行情：
材料单位：
个
材料税率：
地区时间：
深圳市2007年1月信息价
所属行业：
建筑工程
备注说明：

查看价格

联合角咬口机

规格型号：
YZL-16W
价格行情：
材料单位：
个
材料税率：
地区时间：
深圳市2006年6月信息价
所属行业：
建筑工程
备注说明：

查看价格

联合角咬口机

规格型号：
YZL-12B
价格行情：
材料单位：
个
材料税率：
地区时间：
深圳市2006年5月信息价
所属行业：
建筑工程
备注说明：

查看价格

查看详情

第三方软件接口

规格型号：
第三方软件接口
需求量：
1套
报价数：
1
材料品牌：
进口
材料档次：
高档
费用说明：
不含税费 | 含运费
询价时间：
2018-07-30

查看价格

第三方数据对接

规格型号：
对接第三方平台
需求量：
1套
报价数：
1
材料品牌：
海康威尔
材料档次：
中档
费用说明：
不含税费 | 含运费
询价时间：
2019-04-30

查看价格

第三方协议接口

规格型号：
与第三方系统集成
需求量：
1套
报价数：
2
材料品牌：
天创达、西门子、西蒙、施耐德、霍尼韦尔
材料档次：
中档
费用说明：
含税费 | 含运费
询价时间：
2021-06-22

查看价格

河长公示标识

规格型号：
详见图纸大样,不含基础
需求量：
2组
报价数：
3
材料品牌：
无
材料档次：
中档
费用说明：
不含税费 | 含运费
询价时间：
2022-06-30

查看价格

河长公示标识

规格型号：
1.类型:河长公示标识2.材质、规格尺寸:5mm厚中空钢板刷灰色氟碳漆,1530×2200×50mm;5厚50x50方钢面刷紫檀色仿木氟碳漆;名称信息、logo、辅助图案等3.不包含基础4.详见图纸
需求量：
18块
报价数：
3
材料品牌：
无
材料档次：
中档
费用说明：
不含税费 | 含运费
询价时间：
2021-09-15

查看价格

查看详情

角平分线长公式第二形式

角平分线长公式公式 三角形ABC的角平分线为AD，D在CB上。则 角平分线长公式推导过程 证明。如图3，延长AC到E，使CE=CD，连接DE，则AE=AC CD， 。在AB边上取点F，使BF=BD，连接DF，则AF=AB－BD，∠BDF=∠BFD。则 即 又 则 于是 ，便有 ，故 又 由角平分线定理得 即 代入①中得 证毕。

查看详情

角平分线长公式第一形式

角平分线长公式公式 在△ABC中，∠A的角平分线记为 ，∠B的角平分线记为 ，∠C的角平分线记为 ，三边边长为a、b、c，则 其中p是半周长。 角平分线长公式推导过程 证明。法一。如图1，我们先证明 。 由角平分线定理可得 ，并注意到 ，消去 ，化简得 。 由余弦定理， ， 把 和 的表达式代入（1）中， 即 设 ，那么上式可以写成 于是 其他角平分线长度同理可证。 证毕。 提要。法二。运用斯特瓦尔特定理，可得证明。

查看详情

角平分线长公式第三形式常见问题

证明三角形内外角平分线定理

三角形外角定理证明过程; http://zhidao.baidu.com/question/59352008.html?si=1三角形内角定理:(1)角的平分线是到角的两边距离相等的所有点的集合．∠A...
球弧长公式

S=a*3.14*r/180 s为弧长 a为弧长s所对应的圆心角 r为半径
弧长公式是什么

首先来看弧长的计算公式L＝的推导过程：因为360°的圆心角所对的弧长就是圆周长C＝2πR（R为圆的半径）所以1°的圆心角所对的弧长是2πR/360，即。这样n°的圆心角所对的弧长的计算公式是L＝...

查看详情

角平分线长公式第三形式文献

鲁教版六年级下册线段中点与角平分线练习(无答案)

格式：pdf

大小：88KB

页数： 3页

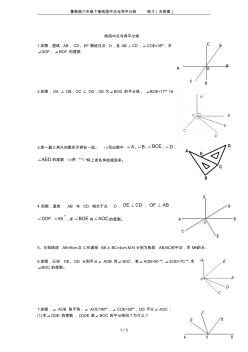
鲁教版六年级下册线段中点与角平分线练习（无答案） 1 / 3 线段中点与角平分线 1.如图，直线 AB、CD、EF 都经过点 O，且 AB⊥CD，∠COE=35°，求 ∠DOF、∠BOF 的度数． 2.如图，OA 丄 OB，OC 丄 OD，OE 为∠BOD 的平分线， ∠BOE=17° 18 3.把一副三角尺如图所示拼在一起。 ⑴写出图中 A、 B、 BCE、 D、 AED的度数；⑵用 “ ”将上述各角连接起来。 4.如图，直线 AB 与 CD 相交于点 O， CDOE ， ABOF ， 65DOF ，求 BOE与 AOC的度数。 5、已知线段 AB=6cm,点 C在直线 AB上,BC=4cm,M,N分别为线段 AB,BC的中点 ,求 MN的长 . 6.如图，已知 OE、OD 分别平分∠ AOB 和∠ BOC，若∠ AOB=90°，∠EOD=70°，求 ∠BOC 的度数。 7.如图，

在线阅读立即下载

三角形边的三等分线分割面积问题证明探究

格式：pdf

大小：88KB

页数： 4页

1问题重现张劲松和刘才华两位老师在文[1]中依次证明了如下结论：如图1,D,E,F,G,H,I分别为△ABC的边BC,CA,AB的三等分点,连接△ABC的顶点与对应的三等分点,把△ABC分成12个三角形、3个四边形、3个五边形和1个六边形,共19个多边形.假设△ABC的面积为1,则19个多边形的面积分别为：研究发现，不但四边形、五边形、六边形都可以通过割补求得其面积，而且上述5个结论，都可以独立的证明（后者的证明不依赖前面已证明的结论）。

在线阅读立即下载

角平分线定理验证推导

已知，如图4，AM为△ABC的角平分线，求证: 角平分线定理面积法 由三角形面积公式，得 S△ABM=(1/2)·AB·AM·sin∠BAM S△ACM=(1/2)·AC·AM·sin∠CAM ∵AM是∠BAC的角平分线 ∴∠BAM=∠CAM ∴sin∠BAM=sin∠CAM ∴S△ABM:S△ACM=AB:AC 根据：等高底共线，面积比=底长比 可得：S△ABM:S△ACM=MB:MC，则AB:AC=MB:MC 角平分线定理相似法 过C作CN∥AB，交AM的延长线于N ∵CN∥AB ∴∠ABC=∠BCN 又 ∠AMB=∠CMN ∴△ABM∽△NCM ∴AB:NC=BM:CM ∵AM是∠BAC的角平分线 ∴∠BAN=∠CAN 又 ∠BAN=∠ANC ∴∠CAN=∠ANC ∴AC=CN ∴AB:AC=MB:MC （过M作MN∥AB交AC于N也可证明） 角平分线定理正弦定理法 作△ABC的外接圆，AM交圆于D 由正弦定理，得 AB:sin∠AMB=MB:sin∠BAM, AC:sin∠AMC=MC:sin∠CAM ∵AM是∠BAC的角平分线 ∴∠BAM=∠CAM 又∠AMB ∠AMC=180° ∴sin∠BAM=sin∠CAM sin∠AMB=sin∠AMC ∴AB:AC=MB:MC

查看详情

角平分线性质定理证明

●三角形内角平分线分对边所成的两条线段，和两条邻边成比例. 即在三角形ABC中，当AD是顶角A的角平分线交底边于D时，BD/CD=AB/AC. 证明 : 如图，AD为△ABC的角平分线，过点D向边AB,AC分别引垂线DE,DF.则DE=DF. S△ABD:S△ACD=BD/CD 又因为S△ABD:S△ACD=[(1/2)AB×DE]:[(1/2)AC×DF]=AB:AC 所以BD/CD=AB/AC. 第一部分 1.角平分线可以得到两个相等的角。 角平分线，顾名思义，就是将角平分的射线。 如右图，若射线AD是角CAB的角平分线，则角CAD等于角BAD。 第二部分 2.角平分线线上的点到角两边的距离相等。 如右上图，若射线AD是∠CAB的角平分线，求证:CD=BD ∵∠DCA=∠DBA ∠CAD=∠BAD AD=AD ∴△ACD≌△ABD ∴CD=BD 第三部分 3.三角形的三条角平分线交于一点，称作三角形的内心。三角形的内心到三角形三边的距离相等。 这一条是第二条的引申，详细证明过程参照第二条和三角形内心。 第四部分 4.三角形一个角的平分线，这个角平分线其对边所成的两条线段与这个角的两邻边对应成比例。 如右下图，平面内任意一小于180度的∠MAN，AS平分∠MAN，直线BC分别交射线AM、AN、AS于B、C、D，求证:AB/BD=AC/CD: 作BE=BD交射线AS于E，如图1: ∵BE=BD， ∴∠BED=∠BDE， ∴∠AEB=∠ADC 又∵∠BAE=∠CAD, ∴△AEB∽△ADC, ∴AB/BE=AC/CD, 即AB/BD=AC/CD. 另外的情况， 如图2，直线BC交AS的反向延长线于D, 如图3，直线BC交AN的反向延长线于C; 此时，仍有AB/BD=AC/CD 证法与图1类似

查看详情

热门搜索

角平分线长公式第三形式

角平分线长公式第三形式

角平分线长公式公式

角平分线长公式推导过程

角平分线长公式造价信息

三角形焊线

三角梅

三角梅

三角托架

三角托架

联合角咬口机

联合角咬口机

联合角咬口机

联合角咬口机

联合角咬口机

第三方软件接口

第三方数据对接

第三方协议接口

河长公示标识

河长公示标识

角平分线长公式第二形式

角平分线长公式公式

角平分线长公式推导过程

角平分线长公式第一形式

角平分线长公式公式

角平分线长公式推导过程

角平分线长公式第三形式常见问题

角平分线长公式第三形式文献

角平分线定理验证推导

角平分线定理面积法

角平分线定理相似法

角平分线定理正弦定理法

角平分线性质定理证明

第一部分

第二部分

第三部分

第四部分

角平分线定理应用例子

相关推荐