连通单元文献

 建筑CAD制图单元二教学设计2.1单元设计
建筑CAD制图单元二教学设计2.1单元设计
建筑CAD制图单元二教学设计2.1单元设计
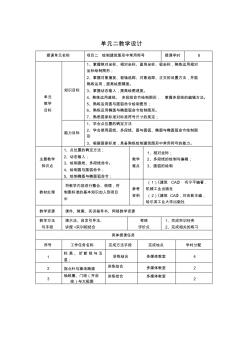
单元二教学设计 授课单元名称 项目二 绘制建筑图形中常用符号 授课学时 8 单元 教学 目标 知识目标 1、掌握绝对坐标、相对坐标、直角坐标、极坐标,熟练运用相对 坐标绘制图形; 2、掌握对象捕捉、极轴追踪、对象追踪、正交的设置方法,并能 熟练运用,提高绘图精度。 3、掌握动态输入,提高绘图速度。 4、熟练运用直线、 多段线命令绘制图形, 掌握多段线的编辑方法。 5、熟练运用圆与圆弧命令绘制图形; 6、熟练运用椭圆与椭圆弧命令绘制图形。 7、熟悉国家标准对标准符号尺寸的规定; 能力目标 1、学会点位置的确定方法 2、学会使用直线、多段线、圆与圆弧、椭圆与椭圆弧命令绘制图 形 3、根据国家标准,具备熟练绘制建筑图形中常用符号的能力。 主要教学 知识点 1、点位置的确定方法; 2、动态输入; 3、绘制直线、多段线命令。 4、绘制圆与圆弧命令; 5、绘制椭圆与椭圆弧命令; 教学 难点 1、相对

 建筑CAD制图单元七教学设计7.1单元设计
建筑CAD制图单元七教学设计7.1单元设计
建筑CAD制图单元七教学设计7.1单元设计
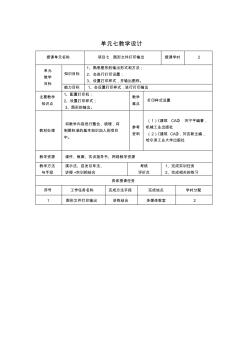
单元七教学设计 授课单元名称 项目七 图形文件打印输出 授课学时 2 单元 教学 目标 知识目标 1、熟悉图形的输出形式和方法; 2、会进行打印设置; 3、设置打印样式,并输出图样。 能力目标 1、会设置打印样式,进行打印输出 主要教学 知识点 1、配置打印机; 2、设置打印样式; 3、图形的输出。 教学 难点 打印样式设置 教材处理 将教学内容进行整合、梳理,将 制图标准的基本知识加入到项目 中。 参考 资料 (1)《建筑 CAD》 巩宁平编著, 机械工业出版社 (2)《建筑 CAD》,刘吉新主编, 哈尔滨工业大学出版社 教学资源 课件、教案、实训指导书、网络教学资源 教学方法 与手段 演示法、启发引导法、 讲授 +实训相结合 考核 评价点 1、完成实训任务 2、完成相关的练习 具体授课任务 序号 工作任务名称 完成方法手段 完成地点 学时分配 1 图形文件打印输出 讲练结合 多媒体教
