离散傅里叶变换文献

 短时傅里叶变换matlab程序
短时傅里叶变换matlab程序
短时傅里叶变换matlab程序
function [Spec,Freq]=STFT(Sig,nLevel,WinLen,SampFreq) %计算离散信号的短时傅里叶变换; % Sig 待分析信号; % nLevel 频率轴长度划分(默认值 512); % WinLen 汉宁窗长度(默认值 64); % SampFreq 信号的采样频率 (默认值 1); if (nargin <1), error('At least one parameter required!'); end; Sig=real(Sig); SigLen=length(Sig); if (nargin <4), SampFreq=1; end if (nargin <3), WinLen=64; end if (nargin <2), nLevel=513; end nLevel=ceil(nLevel/2)*2+1;

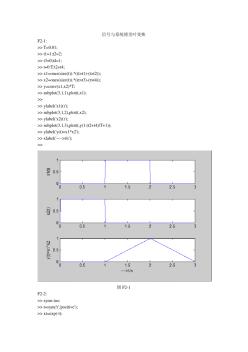 信号与系统傅里叶变换
信号与系统傅里叶变换
信号与系统傅里叶变换
信号与系统傅里叶变换